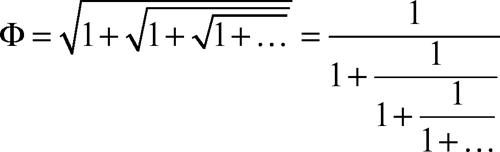successione numerica

successione numerica

successione numerica successione {a_n}, i cui termini sono numeri reali o complessi. Una successione si dice monotòna crescente (decrescente) se per ogni n è a_n ≤ a_n+1 (a_n ≥ a_n+1). Per una data successione {a_n}, si considera il limite

se esso esiste finito si dice che la successione è convergente, se è infinito che è divergente, se non esiste che è indeterminata (o anche che è irregolare; nel caso reale, si usa anche il termine oscillante). Una successione numerica reale è detta limitata se esiste M > 0 tale che

Una condizione necessaria e sufficiente affinché una successione in R o in C sia convergente è che sia una successione di → Cauchy; tale condizione, assai importante, è tuttavia sostituita nelle applicazioni da particolari condizioni sufficienti, dette criteri di convergenza: per esempio in R una successione monotòna ammette sempre limite, che è finito se (e solo se) la successione è limitata. Per il teorema di → Bolzano-Weierstrass da una successione limitata è sempre possibile estrarre una sottosuccessione convergente. Un esempio di successione monotòna è dato dalla successione esponenziale di base a (maggiore di 0 e diverso da 1): se a > 1 la successione {exp_a(n)} è monotòna crescente e per n tendente a +∞ il suo termine n-esimo tende a +∞ e la successione è divergente; se a < 1, la successione è monotòna decrescente ed è limitata inferiormente dal valore 0; la successione è convergente a 0.

Una successione in cui ciascun termine, escluso il primo o i primi, è ottenibile dal precedente (o dai precedenti) attraverso una formula che si ripete a ciascun passo si dice ottenuta (o definita) per ricorrenza. Per esempio, la successione di → Fibonacci {ƒ_n} è così definita per ricorrenza: ƒ₀ = 1; ƒ₁ = 1; ƒ_n = ƒ_n−1 + ƒ_n−2. Una successione ottenuta per ricorrenza dalla formula x_n+1 = φ(x_n), con φ: [a, b] → [a, b] di classe C ¹ e max|φ′(x)| < 1, converge alla soluzione dell’equazione x = φ(x) (teorema delle contrazioni: → Banach-Caccioppoli, teorema di). Per esempio, le successioni definite da

o da

dove x₀ = 1, convergono per n → ∞ al → numero aureo Φ, soluzione dell’equazione

si hanno cioè gli sviluppi

il secondo dei quali rappresenta una frazione continua.

L’insieme s = {x : x = {x_i}_i∈N} di tutte le successioni costituisce uno spazio vettoriale, in cui si può introdurre una metrica ma non una norma. Il sottospazio delle successioni limitate, dotato della norma dell’estremo superiore, ∥x∥ = sup |x_i|, è uno spazio di → Banach indicato con l ^∞.