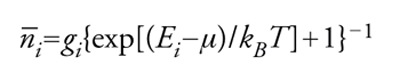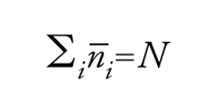statistica di Fermi-Dirac
statistica di Fermi-Dirac
Caratteristica fondamentale di un sistema quantistico composto da un gran numero di fermioni in equilibrio. A differenza del caso della distribuzione di Maxwell-Boltzmann in fisica classica, stati che differiscono solo per lo scambio di particelle identiche non sono considerati distinti per via della indistinguibilità quantistica. La principale peculiarità della statistica di Fermi-Dirac è che il numero di occupazione dei singoli stati (ovvero il numero di particelle che si trovano in uno stato fissato) può avere solo valori 0 o 1, a differenza della statistica di Bose-Einstein (che caratterizza i bosoni), nella quale può essere illimitato. Questa è una conseguenza del principio di esclusione di Pauli, secondo il quale due o più fermioni non possono trovarsi nello stesso stato quantico. In un gas di Fermi ideale (ossia un sistema di fermioni non interagenti) il numero medio n_i di particelle nello stato i (di energia Ei) obbedisce alla distribuzione di Fermi-Dirac
,
dove kB indica la costante di Boltmann, T la temperatura assoluta e μ il potenziale chimico. Quest’ultimo può essere determinato a partire dall’equazione
Il numero gi è il peso statistico dello stato i, ovvero il numero di stati quantici con energia Ei. Il caso più importante è quello di fermioni di spin 1/2, per es. elettroni, in cui gi=2, come conseguenza dell’esistenza di due direzioni possibili per lo spin di una singola particella. La statistica di Fermi-Dirac fu proposta proprio per gli elettroni da Enrico Fermi nel 1929. I suoi fondamenti teorici furono sviluppati poco più tardi da Paul Dirac, che chiarì le sue connessioni con la teoria quantistica. La prima applicazione della statistica di Fermi-Dirac a un gas di elettroni in un metallo fu fatta da Wolfgang Pauli e Arnold Sommerfeld.
→ Superconduttività e superfluidità