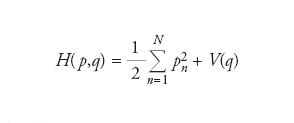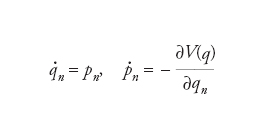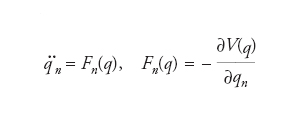spazio delle configurazioni
spazio delle configurazioni
L’uso più consueto del termine si manifesta nel contesto del problema a N corpi in meccanica classica, e in particolare della sua formulazione hamiltoniana, e conseguentemente anche in meccanica statistica. Limitandoci per semplicità, ma senza significativa perdita di generalità, al caso di N particelle puntiformi di massa unitaria in uno spazio unidimensionale, l’hamiltoniana di tale problema si scrive:
dando luogo alle seguenti equazioni hamiltoniane del moto,
e, conseguentemente, alle seguenti equazioni newtoniane,
dove i punti sovrapposti indicano, come di consueto, differenziazioni rispetto al tempo e le lettere p e q identificano vettori a N dimensioni, per es. q≡(q1,…,qN) dove la coordinata qN caratterizza la posizione della particella identificata dall’indice n. In questo contesto per spazio delle configurazioni si intende lo spazio dei vettori a N dimensioni q, sicché a ogni punto di tale spazio corrisponde una configurazione del sistema di N particelle. Analogamente si parla di spazio degli impulsi per lo spazio dei vettori a N dimensioni p e di spazio delle fasi per lo spazio a 2N dimensioni i cui punti sono la coppia di vettori p,q. Una simile terminologia si usa nel contesto dell’analogo problema a N corpi quantistico, in cui la funzione d’onda (nella rappresentazione di Schrödinger) ψ(x) è una funzione del vettore a N dimensioni x le cui componenti corrispondono alle posizioni delle N particelle. Il vettore x può dunque essere identificato con il vettore q, e si può affermare che la funzione d’onda è definita nello spazio delle configurazioni. La trasformata di Fourier della ψ(x) è funzione di un vettore a N componenti k corrispondente (a meno di una rinormalizzazione dimensionale) al vettore p.