Scienza greco-romana. La geometria da Apollonio a Eutocio
Scienza greco-romana. La geometria da Apollonio a Eutocio
La geometria da Apollonio a Eutocio
Il periodo di formazione del canone geometrico greco si estende dal 200 a.C. al 550 d.C., come dire dalla civiltà del Mediterraneo ellenistico, attraverso le trasformazioni della dominazione romana, fino all’epoca dell’egemonia di Bisanzio. Questo canone, nel senso di un corpus ben definito di codici che trattano di matematica, non sarà toccato se non marginalmente nei secoli immediatamente successivi agli anni di Eutocio di Ascalona, i cui commenti ad Archimede e ad Apollonio (una delle aggiunte più tarde alla tradizione canonica) contribuirono a dare al canone la forma definitiva. Dall’VIII sec. in poi fu gradualmente tradotto in arabo e ciò segnò l’inizio della prima vera rinascita della scienza greca, che portò, in definitiva, alla nascita della scienza moderna.
Si può essere quindi tentati di considerare questo periodo come una fase di preparazione, come la strada percorsa dall’Antichità per raggiungere la Modernità; una prospettiva valida, forse la più interessante per l’uomo di oggi. Tuttavia, per arrivare a un’effettiva comprensione storica occorre cercare di capire questo periodo nei suoi propri termini e attraverso gli interessi che esprimeva. Anche se un tale punto di vista non sempre è stato rispettato, alcuni studi recenti sembrano indicare un cambiamento in tal senso (come O’Meara 1989, sull’uso di nozioni matematiche da parte di alcuni filosofi della Tarda Antichità, e Cuomo 2000, su una delle maggiori figure di questo periodo, Pappo di Alessandria). Non vi è però una guida sicura per tutto questo periodo, e la nostra rassegna non può sperare di riempire un vuoto così vasto; presenteremo dunque alcune delle figure più importanti, cercando d’inserire questi autori nel quadro generale delle aggiunte e delle scelte operate in vista della formazione del corpus canonico della matematica greca. Se nessuno di questi è del livello di un Archimede, ve ne sono tuttavia di significativi, come Apollonio, grande matematico di un genere del tutto diverso da Archimede, molto meno indipendente e molto più legato alla tradizione; esamineremo la sua principale opera sui fondamenti, il Libro I delle Coniche, e il suo più importante lavoro originale fra quelli che ci sono pervenuti, il Libro V delle Coniche. Successivamente ci occuperemo di Ipsicle e del Libro XIV degli Elementi, un’ope ra che suggerisce già il tipo di trasformazioni subite dalla matematica greca in questo periodo. Passeremo di seguito all’opera di Pappo, il miglior matematico della Tarda Antichità e per il quale abbiamo il maggior numero di documenti; infine, tratteremo Eutocio, figura rappresentativa del progetto di formazione di un canone nella Tarda Antichità.
Molto verrà tralasciato. Forse l’omissione più vistosa è quella di Diocle, matematico greco che visse a cavallo tra il II e il I sec., autore di uno studio affascinante sugli specchi ustori. Si tratta di uno studio di ottica matematica delle curve fungenti da specchi, che mostra una grande abilità nel trattare questioni di geometria. Quest’opera non soltanto rappresenta un esempio della gamma di problemi a cui danno origine le sezioni coniche (i suoi specchi sono basati principalmente su proprietà delle coniche), ma illustra bene i rapporti tra teoria, pratica e fantasia nel lavoro del matematico (v. cap. XXVI). Va sottolineato però che Diocle, pur essendo l’autore maggiormente compreso, è soltanto uno dei rappresentanti di tutta una generazione di matematici che nel III-II sec. affrontarono problemi complessi all’interno della tradizione archimedea.
È inoltre difficile isolare la geometria dagli altri campi, in particolare dall’astronomia, la disciplina matematica che si può dire sia stata al centro dell’interesse per quasi tutto questo periodo. Oltre allo studio geometrico delle orbite dei corpi celesti, l’astronomia ha altri collegamenti con la geometria, in particolare tramite la trigonometria (necessaria per calcoli approssimati: v. cap. XXII). Un’altra disciplina collegata alla geometria e all’astronomia è la geografia; gli aspetti teorici delle osservazioni geografico-astronomiche hanno spesso portato, in questo periodo e in seguito, a studi di carattere puramente geometrico, per esempio nella teoria degli orologi solari (v. cap. XXV).
Se può sembrare anacronistico attribuire all’opera di un autore come Apollonio un significato che avrà soltanto nella Tarda Antichità, le nozioni di canonicità e tradizione sono invece senz’altro valide. Anche Apollonio, infatti, operava in un contesto nel quale la tradizione era una realtà onnipresente, anche nel senso letterale della parola, poiché scriveva nella Biblioteca di Alessandria. La geometria greca aveva fatto molta strada dall’epoca dei rari rotoli di papiro del V e IV sec.; con Apollonio si entra in un periodo nel quale la storia della matematica greca, nel senso della coscienza storica da parte di chi la pratica, è parte integrante della matematica stessa.
Apollonio e le sezioni coniche
Apollonio nacque probabilmente alcuni decenni dopo Archimede, non sappiamo esattamente quando. Per molti altri aspetti si può pensare ai più grandi geometri greci, Euclide, Apollonio e Archimede, come a una triade nella quale Apollonio, anche se è l’autore più tardo, occupa una posizione intermedia. Se di Euclide conosciamo a malapena il nome, e Archimede è al contrario una figura storica precisa, con date e attività ben chiare, identificare e datare Apollonio è possibile ma non senza difficoltà. Anche per quanto riguarda le caratteristiche della sua opera scientifica, Apollonio occupa una posizione intermedia tra i due. Euclide sembra essersi accontentato di raccogliere un insieme di strumenti basandosi sul lavoro dei suoi predecessori, mentre ad Archimede interessava soltanto introdurre idee nuove e più avanzate; la fama di Apollonio è dovuta invece alle Coniche, un’opera di fondamenti, che in parte è una raccolta di strumenti desunti da matematici precedenti (e dallo stesso Euclide), in parte è un trattato originale che contiene risultati molto profondi.
Vi sono varie ragioni che spiegano perché la sua fama sia dovuta a quest’opera: intanto, si tratta probabilmente della sua opera più consistente, e poi l’argomento è uno dei più fertili della matematica premoderna; tuttavia, più importante di altre considerazioni è il fatto che non sia andata perduta. È l’unica opera di Apollonio a noi pervenuta, anche se soltanto in parte, in greco, grazie a Eutocio che pubblicò un’edizione commentata dei primi quattro libri, conservandoli così in greco per i posteri. Degli otto libri dei quali consta, ne possediamo altri tre in arabo, dal quinto al settimo, i quali, ignoti in Occidente prima del XVII sec., non contribuirono come avrebbero potuto alla Rivoluzione scientifica che avvenne in quel secolo.
Fonti più tarde parlano molto di Apollonio, rinviandoci la figura di un autore prolifico attivo in molti campi della matematica (per il suo contributo all’astronomia, v. cap. XXI), ma di tutto ciò sappiamo poco nei dettagli. A eccezione delle Coniche, abbiamo una buona conoscenza soltanto di un altro gruppo di opere, quelle di cui parla Pappo nel Libro VII della sua Collezione matematica (v. oltre): la Sezione di ragione, la Sezione di area, la Sezione determinata, le Inclinazioni, i Contatti e i Luoghi piani. Soltanto la prima ci è pervenuta, e anche questa soltanto in arabo. Sembra che ognuna di queste opere fosse dedicata a un singolo problema. Nel caso della Sezione di ragione il problema è il seguente: date due rette e fissato un punto su ciascuna di esse, tracciare una retta passante per un punto dato e che stacchi su ciascuna retta segmenti (misurati dal punto fissato) che stanno tra loro in un rapporto dato. È chiaro che questo problema varia a seconda della mutua posizione delle due rette e dei punti; Apollonio, nel corso di due libri, passa meticolosamente in rassegna tutti i casi possibili. Un lavoro impressionante, più però per la sua sistematicità che per l’ispirazione matematica. In questo senso è paragonabile ai Dati di Euclide, anche se quest’ultima opera sembra concepita per scopi ulteriori (e ciò giustifica la presenza di dimostrazioni poco ispirate), mentre la Sezione di ragione non è un punto di partenza bensì di arrivo, che copre completamente un certo campo. La sistematicità diventa così molto più di uno strumento, diventa un modo di affermare una posizione matematica.
Lo stesso vale per le Coniche, l’opera più interessante di Apollonio. Un’opera sulle coniche che forniva le definizioni, le costruzioni e i risultati principali esisteva già, ed era quella di Euclide; non ci è pervenuta, ma non c’è ragione di supporre che il livello di accuratezza fosse inferiore a quello solito di Euclide. Per ogni altro matematico greco ciò sarebbe stato sufficiente, ma non per Apollonio; egli si mise a scrivere i propri Elementi relativi alle coniche, e non contento della prima versione ne scrisse una seconda. Possediamo soltanto quest’ultima, e perciò non siamo in grado di dire il perché di due versioni, né, ciò che più conta, possiamo confrontare il suo progetto con quello di Euclide, poiché l’opera di quest’ultimo è andata perduta. Abbiamo però chiaro a cosa mirasse Euclide con le sue definizioni delle sezioni coniche, e questo può aiutarci a chiarire quali potevano essere le idee di Apollonio.
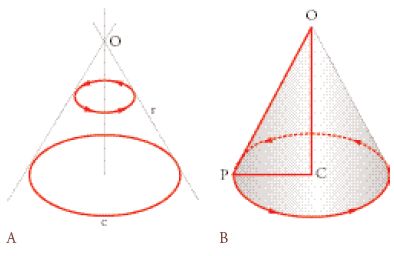
La definizione di cono (più precisamente, di superficie conica) data da Apollonio è la seguente:
Se da un punto [O: fig. 1A] si traccia una retta [r] alla circonferenza [c] di un cerchio che non appartiene allo stesso piano del punto, e la retta è prolungata in entrambe le direzioni, e se tenendo fisso il punto la retta è fatta ruotare intorno alla circonferenza per ritornare alla posizione di partenza, la superficie che risulta generata, composta delle due superfici verticalmente opposte, ciascuna delle quali aumenta indefinitamente prolungando indefinitamente la retta generatrice [r], la chiameremo superficie conica. (Conica, lib. I, def. I)
Confrontiamo questa definizione con quella che Euclide dà del cono negli Elementi:
Cono è la figura che è compresa quando, in un triangolo rettangolo [OPC: fig. 1B], resti immobile uno dei lati comprendenti l’angolo retto, e si faccia ruotare il triangolo intorno ad esso finché non ritorni nuovamente nella stessa posizione da cui si cominciò a farlo muovere. (Elementa, lib. XI, def. 18)
Anche se si basano entrambe su rotazioni, le due definizioni sono essenzialmente differenti; Apollonio pone l’accento sull’infinita estendibilità della superficie conica (cosa difficile da ottenere seguendo la definizione di Euclide) e ne fa una superficie doppia attorno al punto a partire dal quale è generata (per cui il cono di Apollonio risulta una superficie diversa da quella di Euclide). Questa duplice differenza risale alla concezione che Apollonio ha del cono come di un luogo che permette di stabilire relazioni tra le sezioni coniche, queste non essendo considerate come oggetti derivati dal cono; già nel definire il cono Apollonio pensa alle sezioni coniche (per l’iperbole e per la parabola l’estendibilità indefinita è essenziale), e ciò è evidente soprattutto dal nuovo nome che egli dà a queste curve. Euclide aveva utilizzato il sistema, di origini oscure, di chiamare ossitoma, ortotoma e amblitoma le tre sezioni secondo i tre tipi di angolo (v. cap. XVII). Apollonio dà loro i tre nomi che usiamo oggi ossia, rispettivamente, ellisse, parabola e iperbole, che corrispondono a relazioni quantitative (applicazione in difetto, applicazione d’area e applicazione in eccesso) dimostrate nelle propp. 11-13 del Libro I. La vera identità delle sezioni coniche risulta legata ai risultati dimostrati nel libro stesso e in tal modo le Coniche di Apollonio dichiarano di voler essere un’opera sistematica.
Le propp. 11-13 ci portano al cuore della discussione su quest’opera. Il lavoro storico più importante dedicato alle Coniche, dovuto a H.G. Zeuthen, propone un’interpretazione di tipo algebrico dell’impostazione di Apollonio, interpretazione che però è stata contestata dallo stesso Zeuthen (1886). Secondo Zeuthen, le sezioni coniche altro non erano per i Greci se non curve che rappresentavano le relazioni quantitative espresse dalle tre applicazioni in difetto, d’area e in eccesso. La storiografia moderna ritiene invece che Apollonio le intendesse come un tipo particolare di curve; la sua impostazione è caratterizzata dal fatto che queste curve sono considerate da un punto di vista sistematico, distinguendo i vari tipi in base alle loro proprietà, proprietà che sono dimostrate nel trattato. L’opera di Apollonio, dunque, non è più algebrica di quella di Euclide, ma è più sistematica, quindi più ‘astratta’ e di conseguenza più vicina all’impostazione moderna. Zeuthen aveva ragione nel trovare in Apollonio elementi che vanno nella direzione dell’algebra moderna, ma i suoi critici hanno anch’essi ragione nel sottolineare che Apollonio non andava verso Cartesio, verso la matematica moderna, come immaginava Zeuthen, ma piuttosto si allontanava da Euclide restando all’interno della matematica greca.
La questione di ‘cosa sono le sezioni coniche’ non era poi molto importante per i matematici greci. Apollonio, offrendone una presentazione sistematica, approntava una ‘cassetta degli strumenti’; i primi libri delle Coniche erano sviluppati infatti in modo che potessero risultare utili per risolvere problemi complessi. L’utilità delle sezioni coniche nel confrontarsi con simili problemi risiede principalmente nel fatto che le uguaglianze che le definiscono collegano misure lineari e aree. A partire da queste uguaglianze Apollonio determina tutta una serie di importanti risultati, i quali, anche se per la maggior parte erano già noti (specialmente quelli del Libro I) grazie ad Archimede e ad altri autori, sono ora sistematicamente riferiti alle principali uguaglianze relative alle sezioni coniche (Tav. I).
Molte altre uguaglianze si possono poi dedurre introducendo le tangenti alle coniche (concetto non semplice, che Apollonio non tenta di definire rigorosamente). In poche righe si possono ottenere risultati sorprendenti, e cioè uguaglianze (e non soltanto disuguaglianze) che restano invariate anche cambiando i parametri. Questa situazione è tipica delle coniche: la loro grande fecondità nel produrre uguaglianze di questo tipo ne fa l’oggetto preferito della matematica prima dell’avvento dell’analisi.
Di conseguenza, le coniche tendono alla moltiplicazione indefinita dei risultati che le riguardano, ma Apollonio tiene questa proliferazione sotto controllo. La struttura del Libro I è molto chiara e la divisione in sezioni è ben definita: nelle propp. 1-14 (secondo la numerazione di Heiberg) sono dati i risultati principali, e le propp. 15-34 aggiungono altri risultati preliminari, di carattere soprattutto qualitativo, che riguardano tangenti e secanti; in tal modo, pur senza essere in grado di dare una definizione generale di tangente a una curva, Apollonio riesce a fornirne un concetto chiaro attraverso una sistematica accumulazione di risultati. Su questa base, nelle propp. 35-51 è dedotto un primo insieme di uguaglianze per le sezioni coniche. In particolare, la proposizione 51 afferma che se prendiamo un punto E nel piano di una conica, per esempio di una parabola, a volte è possibile tracciare un segmento di retta da E alla conica, per esempio EB, in modo che il segmento da B ortogonale all’asse della conica sia un segmento minimo, ma a volte ciò non è possibile: nessun segmento minimo nel senso ora detto passa per E; d’altra parte, può accadere che da uno stesso punto si possa tracciare più di un segmento in modo tale che le rette intercettate diano luogo a segmenti minimi. Il Libro termina quindi con le propp. 52-60, relativamente indipendenti dalle precedenti, nelle quali il problema di costruire sezioni coniche è risolto sotto varie condizioni, del tipo di quelle della Sezione di ragione. Queste proposizioni costituiscono un piccolo trattato a sé stante e concludono la presentazione sistematica della principale tecnica di risoluzione di problemi della matematica premoderna.
Il Libro V delle ‘Coniche’ di Apollonio
Con il Libro V delle Coniche si comincia in un certo senso a guardare al di là della matematica greca, in primo luogo perché il testo greco degli ultimi quattro libri (V-VIII) è andato perduto, e anzi sembra che fosse già perduto nella Tarda Antichità. Eutocio scrisse un commento ai primi quattro libri delle Coniche, ma non diede seguito al suo lavoro, e forse fu questa l’ultima volta in cui gli otto libri furono visti nel mondo di lingua greca. Tuttavia, alcune copie sono sopravvissute nel Vicino Oriente: già all’inizio del IX sec. l’opera fu tradotta in arabo dai Banū Mūsā; questa traduzione non comprende però l’ultimo libro, l’VIII, che pare sia andato completamente perduto. Le Coniche di Apollonio, nella loro forma quasi completa, ebbero perciò un ruolo essenziale nella matematica araba, che rappresenta lo sviluppo più coerente di quella greca. In Occidente gli ultimi libri erano noti nella descrizione fattane da Pappo (nel Libro VII della Collezione: v. oltre). Soltanto molto più tardi essi furono tradotti dall’arabo e la prima traduzione affidabile fu quella curata da E. Halley agli inizi del XVIII sec.; tuttavia, in quel periodo la matematica europea aveva già superato il punto in cui, oltre l’interesse di tipo storico, poteva trovare alimento nel confronto con le proprie origini greche. Non abbiamo nemmeno testimonianze che ci dicano se nell’Antichità Greca gli ultimi lavori di Apollonio siano stati attentamente letti o sviluppati, a parte il caso isolato di Pappo; i lettori di Apollonio furono soprattutto arabi.
Come la maggior parte dei Greci, Eutocio non è mai andato oltre il Libro IV, e per un semplice motivo: gli ultimi libri, e in particolare il V, sono difficili. La difficoltà è duplice: per prima cosa, s’introducono concetti nuovi, oltre a quello in sé già complicato di conica, come il concetto di ‘retta minima’, che sarà sviluppato nel Libro V. In breve, una retta minima è la retta più corta (come di norma nella matematica greca, ‘retta’ è da intendersi spesso, come qui, ‘segmento di retta’) che si può tracciare da un dato punto a una data conica. Questo concetto non ha applicazioni ovvie, e sembra anzi condurre a un punto morto; il Libro V non si presenta cioè come un invito a ulteriori studi, ma come l’ultima parola su un argomento particolare e chiuso in sé. Apollonio – ed è qui la maggiore difficoltà – punta chiaramente a essere, in senso matematico, conclusivo, per cui questo libro non è soltanto sistematico, ma è anche completo fino all’ossessione. Nel Libro V – un libro di 77 proposizioni, molte delle quali presentano una struttura interna estremamente articolata – si esplorano metodicamente, una dopo l’altra, tutte le possibilità combinatorie offerte dalle differenti sezioni coniche e dal fatto che uno stesso risultato si può dimostrare sotto condizioni diverse e in vari casi particolari per coniche diverse.
Le otto propp. 16-23 mostrano bene l’intenzione di trattare un dato problema in tutti i particolari. Nel quadro delle ‘rette minime’ sono considerate le ‘rette massime’, cioè le rette più lunghe che si possono tracciare da un dato punto a una conica. Si tratta di un caso a sé, perché soltanto le ellissi ammettono rette massime (ogni altra conica ha rami che si estendono all’infinito, per cui nessuna retta da un punto del piano alla conica può mai essere massima). Sembra pertanto che si tratti di un argomento inserito per ragioni di completezza, benché Apollonio mostri alcune relazioni tra rette minime e massime, ovviamente soltanto per le ellissi, collegando in questo modo le due nozioni. Anche in altri casi sono esaminate questioni che riguardano un solo tipo di coniche (per es., le propp. 41-43 sono significative soltanto per l’iperbole); tuttavia, soltanto le rette massime sono così particolarmente legate a una sola conica.
Quando un risultato su rette minime si applica invece a diverse sezioni coniche, anche se con proprietà diverse nei singoli casi, Apollonio si ripete, come capita nelle propp. 58-63, che trattano il problema di tracciare rette minime da un dato punto e la cui soluzione è leggermente diversa a seconda delle diverse coniche e della posizione del punto. Sono completamente risolti sei problemi, indipendentemente l’uno dall’altro, senza sfruttare analogie e connessioni tra i vari casi che avrebbero potuto abbreviare l’esposizione. Inoltre, molti teoremi hanno una struttura complicata, in particolare i due teoremi centrali del Libro V, le propp. 51 e 52 (15 pagine nell’edizione Toomer 1990), le quali presentano il risultato principale del libro: le condizioni sotto le quali si possono tracciare nessuna, una o due rette minime. La discussione è divisa in due parti: parabola (prop. 51), ellisse e iperbole (prop. 52), ciascuna delle quali si suddivide a sua volta in vari sottocasi, a seconda delle condizioni che deve rispettare il numero delle possibili rette minime. Nella prop. 51 Apollonio affronta per prima cosa la non esistenza di rette minime nelle condizioni date, analizzando tre sottocasi di queste condizioni. Considera poi il caso dell’unicità, dimostrando dapprima che una certa retta è minima, e poi – con due dimostrazioni differenti – che due altre possibili rette (da una parte e dall’altra della precedente) non sono minime. Infine, è esaminato, in una sola dimostrazione, il caso in cui esistono due rette minime; la dimostrazione di questa proposizione consta di sette parti e si tratta forse della dimostrazione più complessa e articolata di tutto il canone della matematica greca.
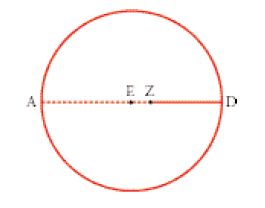
Come spiega lo stesso Apollonio nell’introduzione, le ‘rette minime’ erano già note, ma erano state menzionate soltanto di sfuggita. L’origine di questa nozione è chiara: nel Libro III di Euclide, dedicato al cerchio, vari teoremi trattano di rette minime e massime; per esempio, nella prop. 7 si dimostra che, se Z (fig. 3) è un punto di un cerchio di centro E, ZA è la retta più lunga tracciata dal punto Z al cerchio, mentre ZD è la retta più breve, la minima appunto, essendo AD il diametro passante per Z. Molta parte dello studio delle coniche in Grecia si può considerare una generalizzazione per analogia dal cerchio alle altre coniche e spesso quest’analogia diventa fertile in modo molto interessante. Nell’esempio considerato, mentre è intuitivamente chiaro che la retta più breve spiccata da Z è ZD, non è possibile capire soltanto con l’aiuto della figura qual è la retta più breve diciamo da un punto a una parabola. Nella prop. 8 del Libro V delle Coniche, Apollonio dimostra che questa retta permette di determinare il ‘sintomo’ della parabola, cioè una relazione costante tra certe grandezze che variano a seconda della posizione di un punto della curva e corrisponde talvolta, ma non sempre, all’equazione locale della curva.
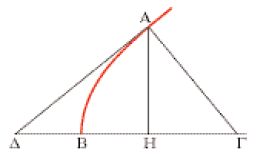
Dopo la ripresa nel mondo arabo, anche ai nostri giorni il Libro V delle Coniche ha ricevuto l’attenzione degli studiosi, che spesso ne hanno però travisato il significato. In alcuni lavori recenti esso è presentato da un punto di vista che può essere illustrato con il seguente esempio. In una serie di proposizioni relativamente autonome e indipendenti (propp. 27-33), Apollonio dimostra che esiste una stretta relazione tra rette minime e tangenti (fig. 4): una retta minima come la AΓ è sempre perpendicolare alla tangente passante per A (cioè l’angolo ΓAΔ è retto) e viceversa, se AΔ è tangente e l’angolo è retto, AΓ è una retta minima per il punto Γ. In altri termini, nel linguaggio della moderna geometria analitica, le rette minime risultano ‘normali’ alla curva. Se il termine ‘normale’ può avere qualche valore mnemonico, parlare delle ‘normali’ per riferirsi alle rette minime di Apollonio è però del tutto fuori luogo, perché Apollonio non considera la perpendicolarità un aspetto essenziale di queste rette, ma semplicemente una loro proprietà, anche se interessante: ciò che conta per lui è il fatto che sono minime.
Apollonio può essere stato spinto a studiare le rette minime da un aspetto interessante dei risultati che le riguardano. La lunghezza della retta HΓ della fig. 4 (analoga alla lunghezza ZE della fig. 3) è la metà della retta che definisce la parabola. Di conseguenza, la costruzione descritta nella prop. 8 non si applica per i punti la cui distanza dal vertice Δ è minore di ΓA; in questo caso è valida la generalizzazione intuitiva della proposizione di Euclide relativa al cerchio, e la retta minima è quella per il vertice. Muovendosi lungo la conica si trova dunque una discontinuità qualitativa interessante: fino a un certo punto la retta minima coincide con l’asse, per poi sollevarsi improvvisamente verso un ramo della conica. Tali discontinuità implicano la presenza di condizioni, indicano cioè che un risultato sussiste soltanto entro certi limiti.
La natura dell’opera è ormai chiara: si tratta di un esercizio chiuso in sé, che prende le mosse da un’analogia con il cerchio come è trattato negli Elementi di Euclide, che si prefigge di analizzare gli aspetti particolari insorgenti nel caso delle coniche, ed è motivato dalle discontinuità di comportamento di queste, che fanno emergere una grande varietà di casi particolari. Inoltre, è un esercizio di classificazione: tutti gli aspetti di un oggetto considerato soltanto di sfuggita dai matematici precedenti sono classificati mediante uno studio spinto fino alla perfezione e definitivo. Apollonio vi rivela il suo tipico carattere, il suo desiderio di completezza e di voler dire la parola definitiva, aspetti che hanno però il difetto di rendere l’opera poco accessibile e stimolante per ulteriori ricerche. L’opera infatti uscì presto di scena nel mondo greco.
Lo studio sistematico della relazione tra curve di vario tipo, spesso attraverso la considerazione di rette a esse normali, è un fatto moderno che Apollonio non anticipò. Egli sarebbe forse stato attratto dal carattere sistematico che questo tipo di studio presenta, ma se ne sarebbe probabilmente tenuto lontano per il suo aspetto aperto e non conclusivo. In ogni modo, non avendo Apollonio questo tipo di interessi, le normali non avevano per lui il significato che hanno oggi. Il problema della natura delle rette minime va dunque di pari passo con quello della natura delle sezioni coniche. L’impostazione di Apollonio non è in alcun modo algebrica, riguarda soltanto aspetti qualitativi di tipo geometrico. Se qua e là nella sua opera si può pensare di cogliere la prefigurazione di un’impostazione più moderna, si tratta di un fatto accidentale, dovuto alla completezza della trattazione; è proprio per questa completezza che alcuni punti possono sembrare vicini o in parte coincidere con impostazioni moderne.
Ipsicle e il Libro XIV degli ‘Elementi’
Fare meglio dei suoi predecessori era una delle motivazioni principali di Apollonio; se questa è una motivazione tipicamente greca, essa è anche un riflesso della specifica posizione di Apollonio in un contesto intellettuale dominato da una tradizione ben precisa. Vi sono nei suoi lavori analogie ispirate agli Elementi, ma vi sono anche definizioni alternative, che si prevede susciteranno critiche a cui si risponde in anticipo mediante una trattazione il più possibile completa.
Una generazione o due più tardi, nel II sec., Ipsicle fa un passo avanti. Con lui tutto si rifà a una matrice tradizionale: egli scrive infatti a partire dalla tradizione e nella tradizione. ‘Nella tradizione’ in senso proprio, perché l’opera principale che abbiamo di lui ha avuto il destino di essere incorporata nella tradizione testuale degli Elementi di Euclide come ‘Libro XIV’ (per un’altra piccola opera di astronomia a noi pervenuta, De ascensione, v. cap. XXII). Se il titolo ‘Libro XIV’ è fuorviante, il contenuto lo giustifica: scritto come commento agli Elementi, questo trattato è sopravvissuto all’interno di una tradizione che conservava le opere non più per il loro valore intrinseco, ma soprattutto per le relazioni che avevano con un canone testuale stabilito. Analogamente esiste nella tradizione testuale un ‘Libro XV’, un’opera della Tarda Antichità di valore molto minore, dove sono contenuti altri commenti agli Elementi.
L’argomento è il Libro XIII di Euclide: Ipsicle studia le relazioni tra i solidi regolari nelle condizioni ivi espresse. Poiché Euclide inscrive i cinque solidi regolari in una sfera di diametro dato, i vari solidi risultano metricamente confrontabili e quindi ci si può chiedere, per esempio, qual è il rapporto tra i volumi di un dodecaedro e di un icosaedro; nulla nella costruzione dei solidi regolari richiede però la presenza di una sfera, e in questo senso essa presenta un aspetto artificiale. È come se Euclide avesse inventato un gioco di società, ‘mettere solidi in una sfera’, al quale Ipsicle intende partecipare.
Il punto cruciale da sottolineare è che Ipsicle non fu il primo a partecipare al gioco. L’introduzione a questo libro (che si rifà al genere ‘introduzione’ iniziato da Archimede) rivela infatti l’importanza decisiva che la tradizione ha per lui; vale la pena riportarla in dettaglio:
Caro Protarco: quando Basilide di Tiro venne ad Alessandria e incontrò mio padre, passò la maggior parte del suo soggiorno con lui, per via del loro comune interesse per la matematica. E una volta, mentre leggevano l’opuscolo di Apollonio sul confronto tra il dodecaedro e l’icosaedro inscritti in una stessa sfera [...] sembrò loro che la dimostrazione di Apollonio non fosse corretta, e quindi, come seppi poi da mio padre, si misero a correggerla e a riscriverla. Dopo qualche tempo mi imbattei in un altro libro pubblicato da Apollonio, che conteneva la dimostrazione di quel fatto [...] Il libro pubblicato da Apollonio è ora accessibile a tutti; è diffuso in una forma che sembra essere il risultato di un’attenta elaborazione avvenuta più tardi. E io [...] ho deciso di dedicarti un trattato in forma di commento, per via della tua abilità nella matematica [...] e la tua intima amicizia con mio padre [...] ma è ora di finire questa introduzione e cominciare con il mio trattato vero e proprio. (Elementa, lib. XIV, 1-5, ed. Heiberg, V, 1, pp. 1-2)
È chiaro che Ipsicle scrive avendo in mente persone e libri ben precisi; il suo interesse è centrato sull’asse costituito da suo padre, Basilide, Apollonio e Protarco. Nell’introduzione si parla di libri e persone, non di solidi e di teoremi. Ipsicle non dice nulla di cosa poteva essere sbagliato nella dimostrazione di Apollonio secondo Basilide e suo padre, ma nota le ‘edizioni’, come quella tarda di Apollonio che aveva trovato. L’opera di Ipsicle è dunque un ‘commento’, non nel senso letterale di accompagnamento all’opera, ma nel senso che dipende dallo studio di altre opere, ed è scritta con la consapevolezza di essere in questo senso ‘secondaria’ rispetto alle fonti originali.
Un’espressione tipica di Ipsicle, che i suoi predecessori non avrebbero mai usato, è la frase finale dell’introduzione («è ora di finire questa introduzione e cominciare con il mio trattato vero e proprio»). Il testo diventa esplicitamente autoreferente. I suoi predecessori cominciavano semplicemente con qualcosa di generale (un’introduzione) per poi passare alle singole dimostrazioni (il trattato), senza sottolineare il passaggio con frasi come quella citata. Ipsicle invece lo sottolinea; per lui ‘introduzione’ e ‘trattato’ sono termini tecnici, ed egli lo dichiara esplicitamente.
Passiamo ora alla descrizione del contenuto matematico del trattato. L’argomento, tra i più attraenti della geometria greca, ha molti e significativi collegamenti con altri campi. Se prendiamo figure e solidi regolari, e li inscriviamo in cerchi e sfere, dalle proprietà del cerchio segue l’uguaglianza di molti lati e di molti angoli (gli angoli al cerchio che sottendono segmenti uguali). Questo può portare a congruenze e similitudini tra triangoli che a loro volta implicano uguaglianze e proporzioni (Taisbak 1982 mostra come questi risultati informino il Libro XIII degli Elementi, e di conseguenza il X). Il risultato più significativo in questo campo è il seguente: «Se s’inscrive in un cerchio un pentagono equilatero, il quadrato del lato del pentagono è uguale alla somma dei quadrati dei lati dell’esagono e del decagono [equilateri] che siano inscritti nello stesso cerchio» (Elementa, lib. XIII, prop. 10).
Si tratta di un’uguaglianza del tutto inattesa, che spinge a chiedersi se uguaglianze del genere sussistano anche per oggetti tridimensionali, ed è forse per questa ragione che è nato il ‘gioco di società’ dei solidi regolari da inscrivere in una sfera. In questo gioco, tutto ciò che interessa è una data sfera con tutti i solidi regolari inscritti in essa, e un cerchio con tutti (potenzialmente) i poligoni regolari inscritti in esso. È tipico della tradizione di ricerca posteriore a Euclide parlare del ‘lato del pentagono’ o dello ‘spigolo del dodecaedro’ senza specificare di quale pentagono o di quale dodecaedro si tratti; si intendono sempre poligoni o solidi inscritti rispettivamente in un dato cerchio o una data sfera e si tratta poi di scoprire le relazioni tra questi oggetti.
Alcuni risultati interessanti risalgono a prima di Ipsicle, ed egli ne dà il dovuto credito agli autori; di ciò che presenta come originale non possiamo sempre dire con certezza quanto effettivamente lo sia. In ogni modo, poiché Ipsicle si colloca esplicitamente nella tradizione testuale, gli autori di risultati noti sono citati (una pratica non usuale prima di lui, per quanto ne sappiamo), ed è il caso di due risultati dovuti ad Aristeo e ad Apollonio.
Aristeo, forse contemporaneo di Euclide (si parla di lui nel quadro della teoria delle sezioni coniche prima di Apollonio), aveva dimostrato che il pentagono del dodecaedro e il triangolo dell’icosaedro, quando i due solidi sono inscritti in una stessa sfera, sono inscritti in uno stesso cerchio. Con questo risultato, due aspetti del ‘gioco’ – solidi in una data sfera e poligoni in un dato cerchio – diventavano, per il dodecaedro e l’icosaedro, direttamente collegati. Questo legame era stato ribadito da un risultato di Apollonio, il quale aveva dimostrato nella seconda edizione della sua opera, in modo giudicato corretto da Ipsicle, che i volumi del dodecaedro e dell’icosaedro stanno tra loro come le aree delle rispettive superfici. Infatti, le due superfici sono equidistanti dal centro della sfera, e dunque se i due solidi sono decomposti al modo di Archimede in piramidi con il vertice nel centro, tutte le piramidi hanno uguale altezza e i loro volumi complessivi sono quindi proporzionali alle ‘basi’, cioè alle superfici dei solidi. Quest’ultimo risultato suggerisce che dal confronto tra le superfici del dodecaedro e dell’icosaedro si possa passare al confronto tra i due solidi. Aristeo suggerisce un’idea per confrontare le due superfici: se i poligoni che compongono la superficie – pentagoni per il dodecaedro e triangoli per l’icosaedro – sono inscritti nello stesso cerchio, basta confrontare il pentagono e il triangolo e tenere conto del diverso numero dei poligoni dei due solidi. È quanto si propone di fare Ipsicle.
Vi sono alcune cose notevoli nello sviluppo di questo programma, in termini sia di contenuto matematico che del modo di presentarlo: per esempio, dopo aver riconosciuto ad Aristeo la paternità del risultato citato, Ipsicle ne dà una propria dimostrazione, sottolineando con ciò che il suo trattato intende muoversi contemporaneamente nell’ambito della tradizione e in quello della ricerca originale. Nello stesso ordine di idee, Ipsicle dà due diverse dimostrazioni di un suo risultato, ed è un caso raro nella matematica greca, dove le dimostrazioni alternative erano in genere proposte nei commenti; è un ulteriore segno della sua posizione intermedia tra la glossa e la creazione, in cui molti risultati originali hanno la brillantezza del gioco dei poligoni e dei solidi regolari (Tav. II).
Questi risultati sono stati trovati un secolo circa dopo Archimede; non si può pertanto dire che dopo Archimede la matematica greca sia entrata in una fase di declino. È anche vero però che questi sviluppi si situano in un contesto già molto diverso da quello di Archimede, molto più legato alla tradizione. Si tratta di un cambiamento qualitativo che con autori come Ipsicle è soltanto agli inizi; il suo punto di arrivo sarà, dopo alcuni secoli, l’opera di Pappo.
La ‘Collezione’ di Pappo
Con Pappo, che fu attivo agli inizi del IV sec. d.C. ad Alessandria, facciamo un salto di cinque secoli, e molto è cambiato dai tempi di Ipsicle. Funzionava ancora la Biblioteca di Alessandria? E quale status avevano avuto gli studiosi in tutto questo periodo? Possiamo soltanto fare congetture, ma è chiaro che assieme ai cambiamenti ci fu anche una certa continuità.
Alessandria faceva parte di quell’area mediterranea che dai tempi di Ipsicle a quelli di Pappo fu governata dalla pax romana, in modo più diretto nel caso di Pappo, ma già sensibile in quello di Ipsicle. È importante segnalare questa stabilità politica perché essa è alla base della continuità delle pratiche culturali di tutto quel periodo. Ipsicle era erede della tradizione greca, che per i cinque secoli successivi fu trasmessa senza soluzione di continuità sempre negli stessi centri, che sempre di più si definivano in termini di partecipazione a questo processo di trasmissione. Essere membro di un’élite culturale ai tempi di Pappo significava dichiararsi erede della classicità greca. Se Ipsicle aveva una sua originalità pur muovendosi tra testi precedenti, Pappo fu essenzialmente un commentatore, un uomo la cui attività intellettuale consisteva nell’utilizzazione del canone letterario. Si può dire che il suo compito principale sia stato quello di affermare il ruolo della matematica nel più generale canone letterario greco.
Alcune opere di Pappo sono esplicitamente dei commenti: un commento all’Almagesto e uno al Libro X degli Elementi; molte sono andate perdute, quelle che ci sono pervenute sono in arabo e non presentano grande interesse matematico o storico. Più significativo è il fatto che il commento al Libro X degli Elementi (in arabo) sia essenzialmente di natura filosofica. È raro trovare un interesse filosofico nella matematica greca precedente, e questo è un altro segno dello sforzo di Pappo di stabilire un contatto con la tradizione letterario-filosofica della vita intellettuale greca. È probabile che egli abbia anche scritto di geografia o su temi filosofici, ma non ne abbiamo testimonianze dirette.
Pappo deve la sua fama soprattutto alla Collezione, una raccolta di otto libri (gli ultimi sette ci sono pervenuti). Anche se nessuno dei libri è in senso stretto un commento, l’opera si inserisce nella tradizione dei commenti: per esempio, nel Libro II – che ci è pervenuto soltanto in parte ed è dedicato alla teoria dei numeri (nel senso della teoria del calcolo numerico) – Pappo non presenta subito le proprie idee. Prende invece le mosse da un’opera di Apollonio sullo stesso argomento (andata perduta) e offre nuove dimostrazioni dei risultati in essa contenuti. Se Ipsicle dava una nuova dimostrazione di un risultato di Aristeo, ma nel quadro di un’impostazione essenzialmente originale, nel Libro II della Collezione vi sono soltanto nuove dimostrazioni. Si parte da risultati noti e invece di generalizzarli si propongono nuove dimostrazioni e soluzioni. A volte tutto quello che si fa è organizzare materiale precedente al modo di un’enciclopedia (come nel caso di alcune curve particolari nel Libro IV o in quello dei solidi regolari nel V); spesso però, come nel Libro III, il materiale esposto è utilizzato per polemizzare con un contemporaneo e criticare la nuova soluzione di un famoso problema geometrico da questi proposta. La spinta alla critica proviene quasi sempre dal fatto che l’autore oggetto della polemica non segue le regole stabilite dalla tradizione. Un altro esempio di questo atteggiamento polemico si trova nella presentazione del Libro V dei solidi regolari, dove Pappo afferma, pur se implicitamente, che questi oggetti (di grande interesse per i filosofi neoplatonici dell’epoca) devono essere lasciati alla competenza dei matematici, e non dei ‘semplici’ filosofi.
Gli ultimi tre libri sono organizzati essenzialmente per argomenti; se è facile definire il contenuto del VI e dell’VIII (le basi matematiche dell’astronomia e della meccanica, rispettivamente), per il VII è più difficile. È per molti aspetti il libro matematicamente più interessante della Collezione (disponibile ora nell’importante edizione di Jones 1986). L’argomento è definito dallo stesso Pappo come ‘il campo dell’analisi’. Benché vi siano molti riferimenti all’analisi nella filosofia greca, Pappo è la principale fonte matematica per quanto riguarda questo metodo.
Che cos’è l’analisi? Essenzialmente, si tratta di un modo di affrontare un problema matematico supponendolo risolto per poi trarre le conseguenze di questa ipotesi (per gli aspetti logici di questo metodo v. Mahoney 1968 e Hintikka 1974). L’analisi ha avuto un ruolo importante nella geometria greca: nelle opere di Archimede e di Apollonio molti problemi sono affrontati dapprima supponendoli risolti per poi tornare indietro e scoprirne le implicazioni. Questo metodo presenta il valore euristico di fornire all’autore un saldo punto di partenza; nel tentativo di comprendere da un punto di vista logico questo valore euristico, alcuni studi moderni hanno fatto riferimento proprio a Pappo e ai suoi brevi commenti sulla storia e la filosofia dell’analisi. Tuttavia, sembra che Pappo non abbia avuto accesso a fonti diverse dalle nostre, per cui la sua interpretazione del metodo dell’analisi è molto personale e poco significativa per la matematica greca classica nel suo insieme.
In breve, il ‘campo dell’analisi’ si può pensare definito dall’insieme dei risultati utili per risolvere problemi geometrici ed è questo che motiva le scelte di Pappo. Esso comprende quindi una vasta raccolta di opere matematiche molto tecniche, poco interessanti in sé ma estremamente utili. Molte opere di Apollonio ci sono note soprattutto tramite questo libro, come per esempio la Sezione di ragione, che esamina nei dettagli e in tutte le possibili combinazioni un problema di carattere generale. Il Libro VII ha dunque carattere strettamente bibliografico: vi si passa in rassegna un insieme di opere, si riportano lemmi, si discutono i limiti di questa o quella soluzione e si fanno commenti di carattere generale. A questo proposito è un problema aperto stabilire se Pappo parli di ‘campo dell’analisi’ riferendosi a un ambito di conoscenze o a un insieme di testi; in quest’ultimo caso il Libro VII sarebbe, letteralmente, un commento a una collezione di trattati, forse messi insieme proprio dallo stesso Pappo.
Poiché l’argomento è di carattere molto tecnico, il commento tende a essere una successione di proposizioni non collegate tra loro, spesso difficili e il cui interesse intrinseco non è ovvio. Consideriamo, per esempio, la prop. 280: «Stia ΔE a EZ come AB sta a BΓ, e EΔ a ΔΘ come BA ad AH. [Dimostrare che] come il solido che ha per base il quadrato di AΓ e come altezza AB sta al solido che ha per base il quadrato di ΔZ e come altezza ΔE, così la somma tra il cubo di AH e quello che ha il rapporto con il cubo di HB uguale a quello tra il quadrato di AΓ e il quadrato di ΓB sta alla somma tra il cubo di ΔΘ e quello che ha il rapporto con il cubo di ΘE uguale a quello tra il quadrato di ΔZ e il quadrato di ZE.
Questo enunciato, molto tecnico e seguito da una dimostrazione altrettanto tecnica, compare in un contesto nel quale non vi sono riferimenti a quadrati o cubi; la dimostrazione precedente tratta infatti di sezioni coniche e la successiva di proprietà astratte di addizioni e sottrazioni. In realtà il contesto è fornito dall’esterno, e cioè dall’opera a cui Pappo in questo caso si riferisce, il libro V delle Coniche di Apollonio. Allo stato delle nostre conoscenze su quest’opera non siamo in grado di precisare in quale punto il lemma di Pappo potesse essere rilevante (forse in qualche relazione semialgebrica ottenuta a partire dai sintomi delle sezioni coniche); in ogni caso, la dimostrazione è tipica della complessità delle Coniche.
Se ci si chiede che senso potesse avere il lavoro di Pappo per un lettore che non avesse accesso all’opera di Apollonio, la risposta è che la Collezione poteva avere senso soltanto per chi avesse accesso a tutto il canone cui si riferiva Pappo; un’opera come il Libro VII costituiva un’affermazione implicita dell’esigenza di conservare questo canone. La Collezione rispecchia la biblioteca personale di Pappo e suggerisce idealmente un canone comprendente argomenti che vanno dalla geometria (sempre al centro della matematica greca) all’aritmetica, all’astronomia e alla meccanica. Oltre a suggerire la formazione di questo canone, Pappo ne avvia l’impostazione mediante una lettura meticolosa basata su una conoscenza profonda delle tecniche matematiche.
Pappo desiderava soprattutto stabilire la propria padronanza del canone e delle tecniche, e ciò spiega sia l’ampia gamma delle sue letture (pressappoco tutta la letteratura disponibile ai suoi tempi), sia la presentazione tecnica. Il risultato fu però che la sua opera diventò illeggibile non appena il canone scomparve dalla circolazione; pochi lessero Pappo e lo capirono. Nel Rinascimento un caso fortunato rese l’opera disponibile per una generazione di scienziati-umanisti, affascinati dalla memoria di conoscenze perdute che essa rappresentava; Pappo ebbe dunque un ruolo nella reviviscenza europea della matematica greca del XVI sec. e oltre. Questo ruolo, in un contesto che mirava a sviluppare ulteriormente una tradizione perduta, era molto diverso da quello originale della conservazione di un elemento non dominante di una tradizione ancora viva, ossia della matematica come parte dell’eredità letteraria e scientifica greca; ironia della sorte, Pappo ebbe più successo nel Rinascimento che nel proprio tempo.
Il Libro V delle Coniche di Apollonio, che è un esempio tipico delle opere commentate da Pappo, è tipico anche perché, come la maggior parte delle opere da lui considerate, andò perduta per la tradizione greca; sarà dunque utile concludere la nostra rassegna della geometria greca con la figura di Eutocio, il matematico che forse è responsabile della perdita del testo greco delle ultime opere di Apollonio.
Eutocio su ‘La sfera e il cilindro’
Sappiamo poco della persona di Eutocio, salvo il luogo di nascita (Ascalona) e la data (primi anni del VI sec. d.C.). La data ci è nota dai personaggi che egli cita, in particolare Ammonio, al quale dedicò la sua opera principale (il commento al De sphaera et cylindro di Archimede). Questa dedica è significativa poiché Ammonio appartiene a un gruppo di neoplatonici abbastanza noti nella Tarda Antichità ai quali si devono commenti al canone filosofico, in particolare alle opere di Platone e Aristotele (Ammonio commentò alcune opere di logica di Aristotele). In questo contesto culturale, alcuni autori del - l’Accademia di Atene del V sec. s’interessarono di matematica per via dell’importanza che essa aveva per Platone e Aristotele: è il caso di Proclo e Marino, che scrissero commenti, rispettivamente, al Libro I degli Elementi e ai Dati di Euclide.
È significativo che tra gli autori a noi pervenuti, quello che usa più spesso la parola ‘geometria’ sia Filopono (un filosofo del VI sec. d.C.) nel corso dei commenti ad Aristotele. Teone e sua figlia Ipazia, attivi ad Alessandria nello stesso periodo, erano anch’essi filosofi della scuola neoplatonica, ma possono anche essere considerati matematici (la versione che ci è pervenuta della Dimensione del cerchio di Archimede potrebbe essere dovuta essenzialmente a Ipazia, v. Knorr 1989). Infine Simplicio, probabilmente contemporaneo di Eutocio, autore di ampi commenti su Aristotele, è la nostra fonte principale per la matematica del V sec. a.C. (v. cap. XVI); il suo commento alla Fisica comprende infatti una dettagliata discussione di un passo nel quale Aristotele sembra riferirsi a Ippocrate di Chio.
Questo genere di interessi intellettuali non è presente invece nei commenti di Eutocio; se egli fa qualche concessione di maniera alla filosofia (il nome di Socrate, ma solamente il nome, è menzionato nell’introduzione al commento al Libro I dell’opera La sfera e il cilindro), non cita nel testo autori di filosofia né discute di problemi filosofici. Il suo interesse è tutto rivolto a chiarire le opere principali del canone matematico in termini matematici. Ogni tanto si trova un excursus storico, ma sempre entro i confini della storia della matematica in senso stretto; ciò non perché Eutocio non avesse una preparazione filosofica (è inconcepibile che un uomo con i suoi interessi non avesse avuto un’educazione in questo senso), ma perché è come se due secoli dopo Pappo un matematico non potesse più sperare di battersi contro la filosofia per rivendicare alla propria disciplina un posto a sé. Nel commento di Eutocio non c’è più la polemica che c’era in Pappo; il progetto di difendere la matematica greca diventa un progetto di salvaguardia e di conservazione: preservare è più importante che lottare.
Gli sforzi di Eutocio in questa direzione ebbero successo, visto che ci è pervenuta la maggior parte dei suoi commenti di cui si ha notizia, assieme a tutte le opere commentate (spesso nella forma in cui Eutocio stesso le aveva conosciute). Si tratta di tre opere di Archimede (La sfera e il cilindro, Libri I e II, Dimensione del cerchio e Piani in equilibrio) e dei primi quattro libri delle Coniche di Apollonio. Mentre è chiaro che fu una sua scelta quella di commentare soltanto i primi e più elementari libri di Apollonio, anche se Eutocio aveva accesso agli ultimi e più avanzati (si era offerto di scrivere anche altri commenti, ma evidentemente la proposta non era stata accolta con entusiasmo), sembra invece che non gli fu possibile accedere ad altre opere di Archimede nella loro integrità; la sua conoscenza di Archimede era perciò più limitata della nostra.
Tenuto conto di questa limitazione, la sua padronanza delle tecniche della matematica classica è veramente notevole. Nella Tarda Antichità i Greci cercavano con tutte le loro forze di plasmare sé stessi secondo il modello di una classicità che veneravano e, in genere, questo tentativo ebbe maggior successo di quelli che saranno fatti più tardi, all’epoca dell’Umanesimo. I commenti di Eutocio sono in una prosa in greco vicina a quella che poteva essere di Euclide o di Apollonio. Imitare la matematica classica era certamente più facile che imitare una tragedia classica e nasce il sospetto che questa facilità di imitazione non fosse estranea all’interesse che Eutocio mostrava proprio per la matematica. La sua padronanza non è però limitata al solo livello linguistico; il compito che egli si propone è infatti quello di chiarire le dimostrazioni di Archimede e Apollonio. Compito non facile, poiché entrambi gli autori enunciavano lemmi senza dimostrarli oppure fornivano dimostrazioni lacunose, lasciando i dettagli al lettore. Quest’opera di chiarificazione era stata intrapresa anche da Pappo, su scala molto più grande, nel Libro VII della Collezione. Pappo ed Eutocio erano nel complesso molto competenti sia nello scoprire le lacune in un argomento, sia nel provvedere a sanarle. Il testo di Eutocio ebbe più successo, se non altro perché era dichiaratamente un commento che seguiva passo passo il testo di Archimede – formando con questo un tutto coerente – e come tale fu accolto. Se è possibile che il commento ad Apollonio (certamente quello che ebbe meno successo) sia stato tramandato soltanto come un insieme di annotazioni a margine del testo, i commenti ad Archimede sono sopravvissuti come trattati autonomi allegati al corpus archimedeo.
L’opera più ambiziosa di Eutocio è il commento al Libro II dell’opera La sfera e il cilindro di Archimede, un lavoro di volume triplo del trattato commentato. La differenza di mole è dovuta non soltanto alla complessità degli argomenti contenuti nello scritto archimedeo (che richiedono numerose spiegazioni), ma soprattutto a due excursus di particolare importanza per la nostra comprensione della matematica greca. Entrambi prendono le mosse dal tipico problema al quale si trova di fronte un commentatore: una lacuna in un argomento. In un caso, Archimede chiede di trovare due segmenti che stiano in proporzione continua con due altri segmenti dati; nell’altro afferma che un certo problema è risolto una volta che ne sia stato risolto un altro (che in seguito chiameremo il ‘problema perduto’ di Archimede), ma tralascia di fornire la soluzione di quest’ultimo e promette di darla in un’appendice al trattato, che però andò perduta già prima di Eutocio.
Il primo problema è equivalente a quello della duplicazione del cubo (v. cap. XVII); Archita fu forse il primo a proporne una soluzione, dunque molto prima di Archimede, e altre soluzioni, nello spirito di competizione di cui ha parlato W.R. Knorr, furono trovate nei secoli successivi. Enunciato il problema, Eutocio non si limita all’osservazione di carattere matematico che il problema ammette soluzione, o a quella di carattere storico che il problema era stato risolto prima di Archimede, ma redige un catalogo completo delle soluzioni a lui note (dodici), che riporta quasi tutte interamente (anche se purtroppo tradotte nel linguaggio matematico standardizzato della cui padronanza Eutocio andava tanto fiero). È grazie a questo catalogo che possediamo la soluzione di Archita e molte altre testimonianze essenziali per la storia della matematica greca, fra le quali il frammento più corposo che ci sia pervenuto di Eratostene (v. cap. XXV).
Il secondo excursus comprende una testimonianza ancora più interessante. Se nel caso della duplicazione del cubo Archimede non si era preoccupato di fornire una propria soluzione, invece aveva promesso di risolvere il ‘problema perduto’. Toccava quindi a Eutocio andare alla ricerca di questo problema, non soltanto nel senso matematico di trovarne una soluzione, ma anche nel senso filologico di ritrovare il testo originale. S’imbatté in un raro trattato che con tutta probabilità doveva contenerlo, e riportò così all’interno del proprio commento un breve trattato completo di Archimede, andato perduto nella principale tradizione testuale archimedea. A un commento molto particolareggiato a questo trattato Eutocio aggiunse poi due soluzioni al ‘problema perduto’ dovute a matematici ellenistici, i quali di fronte alla stessa difficoltà del testo incontrata da Eutocio, essendo matematici e non commentatori, avevano voluto fornire una propria soluzione. Questo excursus è perciò di grande interesse storico: anche se il commento di Eutocio alla soluzione di Archimede non è particolarmente profondo dal punto di vista matematico (come d’altra parte non lo sono altri risultati), è comunque ben fatto e illustra egregiamente il suo contributo e quello di altri autori del suo tempo allo sviluppo della matematica greca.
La soluzione di Archimede poggia sulle relazioni tra un’iperbole e una parabola tangenti tra loro. In un punto della dimostrazione si fa vedere che un punto T sull’iperbole è ‘sopra’ la parabola; per Archimede è immediato che questo fatto sia vero per tutti i punti dell’iperbole, eccetto il punto di tangenza delle due curve. Nel tentativo d’inserire i dettagli che Archimede aveva trascurato, Eutocio aggiunge la dimostrazione per un altro punto, opposto al primo rispetto al punto di tangenza P. Con una dimostrazione del tutto equivalente a quella data da Archimede per il punto T, si fa vedere che anche P si trova ‘sopra’ la parabola (Netz 1999). Se in questo caso il commento di Eutocio può sembrare banale, esso permette però di porre in luce un fatto che Archimede non evidenzia, e cioè che c’è una simmetria di comportamento delle due curve intorno al punto di contatto, per cui i punti di queste curve si possono mettere sistematicamente in corrispondenza l’uno con l’altro. È questo un aspetto tipico della tradizione dei commenti; non tanto la presenza di osservazioni originali, quanto l’aggiunta di particolari riguardanti possibili relazioni esistenti tra fatti osservati dagli autori delle opere commentate. Queste relazioni possono essere matematicamente molto significative; mettendole in evidenza nei loro commenti Eutocio e altri autori della Tarda Antichità hanno indicato la strada per lo sviluppo della matematica araba e della prima matematica moderna.
Il progresso della matematica moderna, basato sulle applicazioni degli sviluppi più recenti e sulla produzione di teorie sempre nuove, è stato possibile soltanto grazie a una comunità di matematici fortemente interattiva, di studiosi che comunicavano tra loro e potevano disporre della stampa. Nell’Antichità non esistevano comunità del genere, e ciò spiega la natura statica della geometria greca. Negli ottocento anni trascorsi tra Archimede ed Eutocio, malgrado la continuità culturale nel Mediterraneo orientale, poco di qualitativamente nuovo fu prodotto, anche se numerose opere, spesso di alto livello, videro la luce. La galleria di personaggi che abbiamo passato in rassegna non fa giustizia della varietà che presenta l’attività nel campo della geometria in quel lungo periodo, della quale attività possediamo testimonianze soltanto in piccola parte. Tuttavia, non bisogna pensare che la matematica prodotta sia stata quantitativamente così grande; è raro infatti trovare riscontri di un’attività che coinvolgesse più di una piccola minoranza di studiosi. Certo, era una cultura che non poteva usufruire della stampa, per cui anche il numero delle opere che circolavano era molto piccolo; in questo arco di tempo, per esempio, nessun matematico ha lasciato opere reperibili in papiri egizi, benché proprio in Egitto la matematica greca avesse trovato il proprio centro. In un certo senso, pertanto, non è sbagliato rappresentare la geometria greca di questo lungo periodo mediante una serie di personaggi.
Ci siamo soffermati su alcune opere isolate, nel tempo e nello spazio ma anche nel contenuto, e il cui solo contesto comune era il passato cui esse facevano riferimento. È questa la realtà della geometria greca: individui isolati, già a partire da Apollonio e poi sempre di più, da Ipsicle fino a Eutocio; singoli individui che riscoprivano il passato matematico quasi da soli, sforzandosi di dimostrare di farne parte affermando un proprio modo di appartenere alla tradizione di tutta la cultura greca. Il fatto cruciale è infatti che la matematica non diventò mai centrale nella definizione dell’identità greca. Si è trattato di una specie di corsa a staffetta nella quale però ogni corridore raccoglieva il testimone da zero, portando con sé sempre meno man mano che la corsa andava avanti. Non siamo però di fronte a un quadro di ‘decadenza matematica’: isolamento non significa necessariamente decadenza. Archimede era isolato quanto Ipsicle e forse di più. Entrambi poterono probabilmente contare soltanto sul proprio padre come tutore in matematica, anche se Ipsicle aveva in più la fortuna di vivere ad Alessandria. L’isolamento è compatibile con il genio. Certo, si sarebbero potuti formare molti altri Archimede, ma anche un genio isolato può produrre molto. Partendo da zero il matematico greco doveva impadronirsi di una certa tecnica e poi applicarla. La matematica greca tendeva per sua natura a fermarsi a questo livello qualitativo, il livello dell’‘applicazione della tecnica’, al massimo quindi all’applicazione della teoria delle coniche.
Mentre in un certo senso la matematica greca cessava di svilupparsi, la staffetta continuò e le opere principali della geometria si conservarono nella traduzione in arabo. La geometria poté così inserirsi in un contesto come quello del mondo arabo, nel quale la scienza era parte integrante della cultura; la versione araba di un passato scientifico riscoperto permise poi di aprire una nuova fase, concretamente produttiva, per quella che restava essenzialmente scienza greca.
Bibliografia
Cuomo 2000: Cuomo, Serafina, Pappus of Alexandria and the mathematics of late antiquity, Cambridge-New York, Cambridge University Press, 2000.
Hintikka 1974: Hintikka, Jaakko - Remes, Unto, The method of analysis, its geometrical origin and its general significance, Dordrecht-Boston, D. Reidel Publ. Co., 1974.
Knorr 1989: Knorr, Wilbur R., Textual studies in ancient and medieval geometry, Boston, Birkhäuser, 1989.
Mahoney 1968: Mahoney, Michael, Another look at Greek geometrical analysis, “Archive for history of exact sciences”, 5, 1968, pp. 318-348.
Netz 1999: Netz, Reviel, Archimedes transformed: the case of a result stating a maximum for a cubic equation, “Archive for history of exact sciences”, 1999.
O’Meara 1989: O’Meara, Dominic J., Pythagoras revived. Mathematics and philosophy in late antiquity, Oxford, Clarendon Press; New York, Oxford University Press, 1989.
Taisbak 1982: Taisbak, Christian Marinus, Coloured quadrangle: a guide to the tenth book of Euclid’s Elements, Copenhagen, Museum Tusculanum Press, 1982.
Vogel 1963: Vogel, Martin, Die Enharmonik der Griechen, Düsseldorf, Verl. der Ges. zur Förderung der Systematischen Musikwiss., 1963, 2 v.; v. I: Tonsystem und Notation; v. II: Der Ursprung der Enharmonik.
Zeuthen 1886: Zeuthen, Hieronymus George, Die Lehre von den Kegelschnitten im Altertum, Køpenhagen, Höst, 1886.