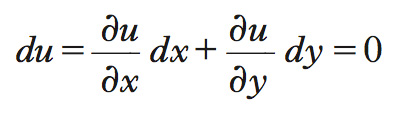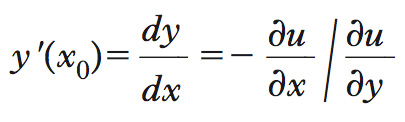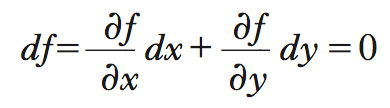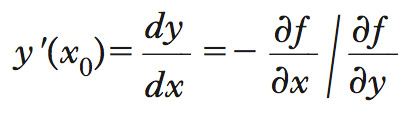saggio
saggio
Rapporto fra due quantità, sinonimo di tasso (➔). I s. o tassi di interesse (➔ interesse p) e di sconto (➔) hanno la dimensione del puro numero, cioè di un rapporto fra quantità omogenee; per es., il s. di interesse del 4% per anno è un rapporto I/C fra un importo di interesse e uno di capitale, ambedue espressi in euro (o in altra valuta comune ai due importi).
I s. di cambio hanno invece la dimensione del rapporto fra monete: per es. il s. di cambio fra euro e dollaro pari a 1,2257 ha la dimensione del rapporto dollaro/euro, ossia 1,2257 dollari per un euro.
I saggi marginali nella teoria dell’equilibrio economico generale
Grande importanza in economia hanno i s. marginali nella teoria neoclassica (➔ neoclassica, teoria) dell’equilibrio economico generale. Il s. marginale di sostituzione è il rapporto in cui due beni di consumo si sostituiscono fra loro lungo una curva di indifferenza (➔), cioè mantenendo inalterato il valore della funzione di utilità (➔ utilità, funzione di p) del consumatore.
Formalmente, indicando con u(x,y) tale funzione, i cui argomenti sono le quantità x,y di due beni (supposti, per semplicità, a un livello costante tutti gli altri), e con u(x,y)=c la linea di livello c della funzione stessa (insieme delle combinazioni che determinano lo stesso livello c di utilità), il s. marginale di sostituzione in un certo punto (x0,y0) si deduce imponendo che sia ivi nullo il differenziale (➔) della u, cioè che sia
Il s. marginale di sostituzione è la derivata
calcolata in (x0,y0); geometricamente esso è l’inclinazione o coefficiente angolare (negativo) della retta tangente nel punto (x0,y0) alla curva u(x,y)=c=c0 =u(x0,y0) e si può interpretare come l’opposto del reciproco del numero di unità aggiuntive di x necessarie per compensare, a utilità invariata, la diminuzione di una unità di y. Per es., se esso è uguale a −1/3 (cioè opposto del reciproco 3), bisogna aggiungere 3 unità di x per compensare la perdita di una unità di y. La stessa impostazione conduce a definire il s. marginale di trasformazione come rapporto in cui due beni si sostituiscono lungo una curva di trasformazione che descrive l’insieme delle possibili produzioni, ottenute impiegando un dato stock di fattori produttivi. Una particolare curva di trasformazione è quella, di equazione f(x,y)=c, che corrisponde al pieno impiego dei fattori produttivi disponibili. Il s. marginale di trasformazione in un certo punto (x0,y0) di tale curva si deduce imponendo che sia ivi nullo il differenziale della f, cioè che sia
Il s. marginale di trasformazione è la derivata
calcolata in (x0,y0); anche esso è l’inclinazione o coefficiente angolare (negativo) della retta tangente nel punto (x0,y0) alla curva f(x,y)=c0=f(x0,y0) e si può interpretare come l’opposto del numero di unità del bene y che debbono essere sacrificate per produrre (mantenendo condizioni di pieno impiego dei fattori produttivi) una unità aggiuntiva del bene x. Nelle usuali condizioni sulla forma delle curve di utilità e di trasformazione di un’economia, l’equilibrio economico si raggiunge quando il s. marginale di sostituzione eguaglia il s. marginale di trasformazione e ambedue sono uguali al rapporto fra i prezzi dei prodotti.