rodonea

rodonea

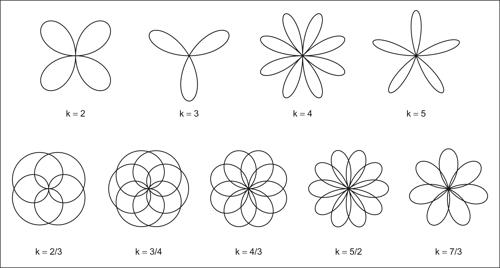
rodonea curva di equazione, in coordinate polari, ρ = Rsinkθ, il cui grafico, contenuto in una circonferenza di raggio R, è costituito da una serie di avvolgimenti intorno al suo centro. Il parametro k determina la forma della curva. Se k è razionale la curva è algebrica e, dopo un numero finito di avvolgimenti, si richiude sul punto iniziale. In taluni casi gli avvolgimenti producono delle figure a forma di rosone, donde il nome, con un numero variabile di petali. Se k è irrazionale la curva è trascendente e risulta costituita da infiniti avvolgimenti che non si richiudono mai sul punto iniziale; la rodonea è allora un caso particolare di → ipocicloide. Se k è intero, la rodonea ha forma di un fiore con k petali se k è dispari, 2k petali se k è pari. Nel caso di k intero, la rodonea può avere pertanto o un numero dispari di petali o un numero di petali multiplo di 4 (doppio di un numero pari). Da ciò segue, per esempio, che non possono esistere rodonee con 6, 10 o 14 petali. In generale, una rodonea non può avere un numero di petali pari a 4h + 2 = 2(2h + 1), ∀h ∈ N.

Se k = 1 la curva è costituita da un solo petalo (una circonferenza di diametro R), l’area della superficie racchiusa dalla curva è

Se k è razionale, se risulta cioè k = n/m con n, m interi, i contorni dei petali si intersecano.