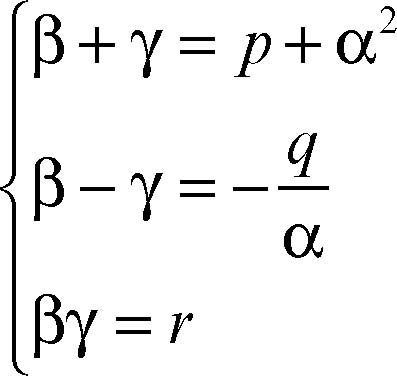risolvente

risolvente

risolvente in algebra, termine sinonimo di equazione risolvente, cioè equazione ausiliaria mediante la quale si rende più agevole la risoluzione di un’altra data equazione. Un primo esempio di risolvente si trova già implicitamente nella Géometrie di Cartesio, nella sua dimostrazione che un problema classico relativo al quadrato, da lui considerato e che conduceva a un’equazione di quarto grado irriducibile, poteva tuttavia essere risolto con riga e compasso. A tal fine egli associa all’equazione di quarto grado una equazione di terzo grado, sua risolvente; utilizzando una radice di quest’ultima equazione le soluzioni dell’equazione data si possono ottenere risolvendo due equazioni di secondo grado. Questo risultato connesso a un caso particolare ha una sua generalizzazione: se l’equazione di quarto grado ha la forma

si suppone di poterla riscrivere nella forma

In tal caso si ottiene il sistema:

Dalle prime due equazioni si ottiene:

Tenendo conto della terza equazione del sistema, si ottiene una equazione di terzo grado in α²:

Una soluzione di questa equazione consente di ottenere le soluzioni dell’equazione originale, risolvendo due equazioni di secondo grado: se si può ottenere α² con al più l’estrazione successiva di radicali quadratici, tale proprietà si estende anche all’equazione di quarto grado data.

Il ricorso a una risolvente per la risoluzione di un’altra equazione, ipotizzato da Eulero e sviluppato da J.-L. Lagrange, venne utilizzato da G. Malfatti per un’equazione di quinto grado: la sua risolvente (risolvente di Malfatti) è un’equazione di sesto grado, la conoscenza di una radice della quale permette la completa risoluzione dell’equazione data (anche se tale risoluzione non può eseguirsi per radicali). Il risultato di Malfatti fu poi ripreso e sistematizzato da E. Galois: la risolvente di Galois di una data equazione algebrica ƒ(x) = 0, è una particolare equazione algebrica collegata alla sua risoluzione, tale cioè che la conoscenza di una sua radice permette di trovare le radici dell’equazione ƒ(x) = 0. Sintetizzando il metodo di Galois, ci si può riferire a una equazione a coefficienti in un campo K (che per semplicità si può supporre sia Q) e si indicano con x₁, x₂, ..., x_n le sue radici che si suppongono distinte. Sia V(x₁, ..., x_n) una loro espressione razionale che si suppone assuma valori diversi per le n! permutazioni di x₁, ..., x_n. Se si indicano con s₁, ... s_n! le sostituzioni in questione, e con

gli n! valori che assume la V al variare degli s_i, si pone:

Questa è un’equazione di grado n! nella variabile y che è la risolvente di Galois di ƒ(x) = 0.

☐ In analisi funzionale, il termine indica un operatore definito da (T − λI)⁻¹, essendo T un operatore lineare limitato su uno spazio di Banach complesso E, I l’operatore identità e λ un numero complesso appartenente all’insieme risolvente di T, ossia all’insieme dei numeri complessi per cui l’operatore inverso è limitato e ha per dominio E.