quadrilatero
Matematica
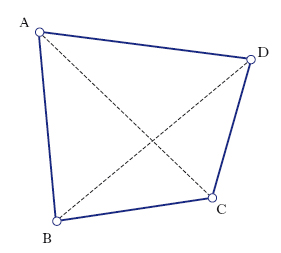
In geometria elementare, la figura individuata da 4 punti (vertici) di un piano, considerati in un dato ordine, e dai 4 segmenti (lati) che li congiungono in quell’ordine; il termine è sinonimo di quadrangolo. Dei segmenti AB, BC, CD, DA che congiungono 4 punti A, B, C, D (fig. 1), i lati AB, CD si dicono opposti, e così i lati BC, DA; similmente sono opposti i vertici A,C e B,D. I segmenti AC, BD si chiamano diagonali. Se i lati opposti hanno punti comuni, il q. si dice intrecciato, altrimenti non intrecciato. Casi particolari del q. sono: il trapezio (q. con 2 lati opposti paralleli), il parallelogramma (q. in cui i lati opposti sono tra loro paralleli), il rombo (parallelogramma con tutti i lati uguali), il rettangolo (parallelogramma con tutti gli angoli retti), il quadrato (lati tutti uguali e angoli tutti retti).
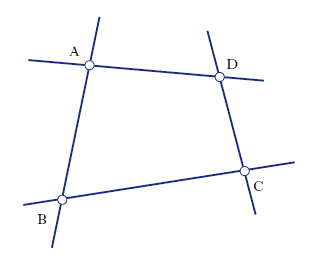
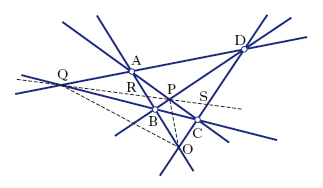
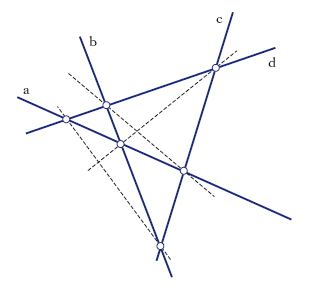
Nella geometria proiettiva, quadrangolo è l’insieme (fig. 2) delle 4 rette AB, BC, CD, DA (lati) che congiungono i punti A, B, C, D (vertici), in quest’ordine. Quadrangolo piano completo è la figura (fig. 3) costituita da 4 punti A, B, C, D di un piano (vertici), a 3 a 3 non allineati, e dalle 6 rette che li congiungono a 2 a 2 (lati); le coppie di lati AB, CD; AC, BD; AD, BC si dicono coppie di lati opposti; i 3 punti d’incontro di coppie di lati opposti (O, P, Q) si dicono punti diagonali e sono vertici di un triangolo che si dice triangolo diagonale del quadrangolo. Q. piano completo (figura duale del quadrangolo piano completo) è l’insieme di quattro rette a, b, c, d, di un piano, non passanti a 3 a 3 per un medesimo punto, e dei 6 punti d’intersezione di tali rette a 2 a 2, che si dicono vertici del q.; le congiungenti coppie di vertici (che non siano lati), si dicono rette diagonali e sono lati di un trilatero che si dice trilatero diagonale del q. (fig. 4).
Tecnica
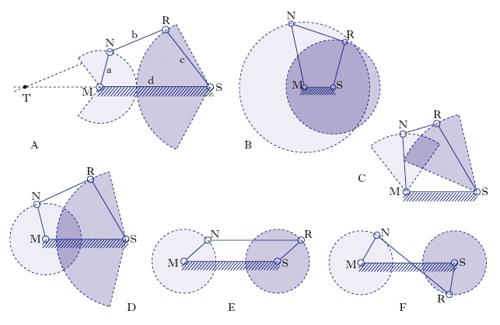
In meccanica applicata, q. articolato, la catena cinematica chiusa e semplice di 4 membri (aste, lati) accoppiati mediante 4 coppie rotoidali M, N, R, S (cerniere). Se gli assi delle coppie rotoidali sono paralleli si ha il q. articolato piano (fig. 5A); se gli assi delle coppie rotoidali sono incidenti in un punto si ha il q. articolato sferico, di cui un caso particolare e notevole è costituito dal giunto cardanico.
Con riferimento al q. articolato piano, se si suppone di tenere fermo uno dei membri, per es. MS, la catena dà origine a un meccanismo; il membro fisso si chiama telaio o ponte; i membri a esso contigui, MN, SR, hanno moto rotatorio e prendono il nome di bilanciere o di manovella a seconda che non possano compiere una rotazione completa (nel qual caso il loro moto è oscillatorio: fig. 5A) o la possano compiere (nel qual caso il loro moto è continuo: fig. 5B); il membro NR è dotato di un moto più complesso e si dice biella. Per una posizione generica del meccanismo il rapporto tra le velocità angolari ωA e ωB dei membri rotanti MN e SR è dato da ωA/ωB=ST/NT, dove T è l’intersezione dell’asse della biella con l’asse del telaio. In base alle relazioni tra le lunghezze delle varie aste, e in base all’asta che assume l’ufficio di telaio, si hanno configurazioni caratteristiche del q. articolato. Se si indicano con a, b, c, d le aste e con le medesime lettere si indicano anche le loro lunghezze disposte in ordine crescente (a≤b≤c≤d), si hanno due casi fondamentali a seconda che la somma delle lunghezze dell’asta più corta e dell’asta più lunga sia maggiore (a+d>b+c) oppure minore o uguale (a+d≤b+c) della somma delle lunghezze delle altre due. Quando è valida la prima relazione, si ha un meccanismo di doppio bilanciere, qualunque sia l’asta che assume l’ufficio di telaio (fig. 5A). Quando è valida la seconda relazione, se si tiene fisso il membro più corto si ha il meccanismo di doppia manovella (fig. 5B), se si tiene fisso il membro opposto al più corto si ha il meccanismo di doppio bilanciere (fig. 5C), se si tiene fisso uno dei membri contigui al più corto si ha il meccanismo di manovella e bilanciere (fig. 5D). Questa distinzione di configurazioni caratteristiche, sulla base delle relazioni prima ricordate, è nota come regola di Grashof.
Il caso particolare di validità dell’uguaglianza nella seconda relazione si verifica certamente quando il q. articolato ha le aste opposte a due a due uguali; il meccanismo può assumere in tal caso la configurazione di un parallelogramma articolato (lati opposti paralleli: fig. 5E) o di un antiparallelogramma articolato (q. intrecciato: fig. 5F). Il meccanismo si comporta in entrambi i casi come meccanismo di doppia manovella, con rotazioni delle manovelle concordi o discordi. Posizioni singolari del q. articolato sono quelle di punto morto, cioè quelle per le quali 2 (o più) aste sono allineate. Tali posizioni corrispondono alle posizioni limite delle oscillazioni dei bilancieri (ove questi siano presenti).