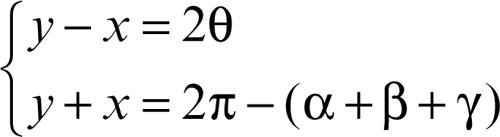Snellius-Pothenot, problema di
Snellius-Pothenot, problema di
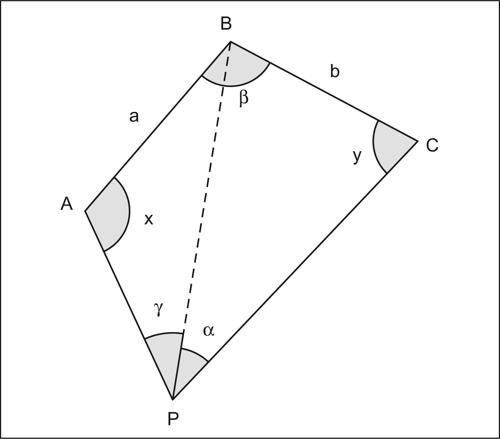
Snellius-Pothenot, problema di problema di topografia che consiste nel determinare la posizione di un punto P rispetto a tre punti dati A, B e C, dei quali è nota la posizione, tali che A, B, C e P siano complanari. Noti
e misurati gli angoli
il problema è risolto una volta che si siano trovati gli angoli incogniti
Applicando il teorema dei → seni ai triangoli BAP e BCP e posto
si trova
da cui, applicando le proprietà del comporre e dello scomporre (→ proporzione) e attraverso ulteriori manipolazioni algebriche, si ottiene
Posto infine
si ottengono i valori cercati di x e y come le soluzioni del sistema
Se α + β + γ = π, allora il problema è indeterminato. Il problema fu posto e risolto attorno al 1615 dal matematico e astronomo olandese W. Snell (latinizzato in Snellius). È noto anche come problema di Pothenot perché fu riproposto nel 1695 dal matematico francese L. Pothenot, che lo risolse con differenti metodi analitici.
Il problema di Snellius-Pothenot è anche noto come problema semplice di Snellius-Pothenot per distinguerlo da una sua generalizzazione che riguarda la determinazione di un qualunque numero intero positivo n di punti di un piano, nota che sia la posizione di tre punti dati nel piano stesso.
