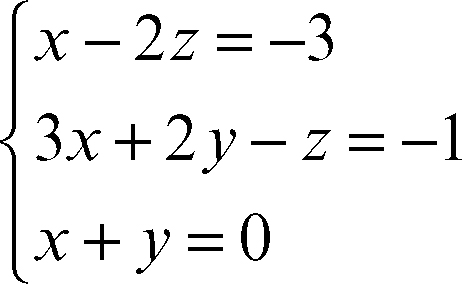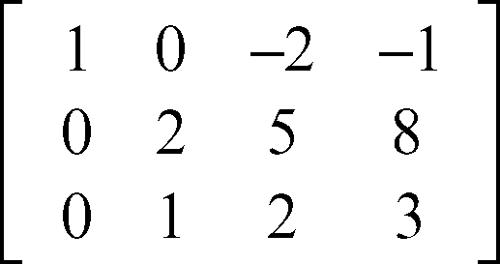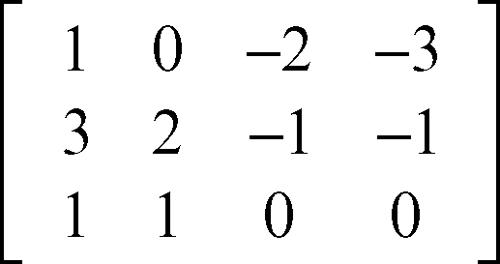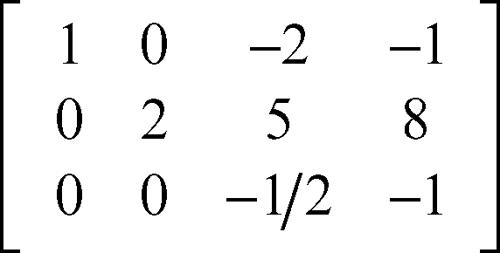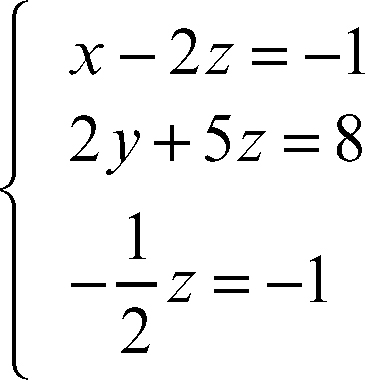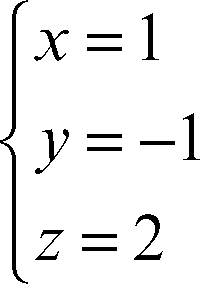pivot

pivot

pivot in algebra lineare, e soprattutto nelle applicazioni della matematica all’economia relative alla programmazione lineare che coinvolgono trasformazioni di matrici, è l’elemento di volta in volta utilizzato come valore di riferimento per raggiungere l’obiettivo desiderato. Data una matrice m × n, è possibile trasformarla in matrice a scalini mediante un procedimento iterativo (→ Gauss-Seidel, metodo di), effettuando successive operazioni sulle righe, facendo appunto uso del pivot, che rappresenta di volta in volta l’elemento di riferimento per la trasformazione. Data una matrice con elemento a₁₁ ≠ 0, questo stesso elemento diventa il primo pivot per fare in modo che tutti gli elementi della colonna a esso sottostanti diventino nulli. Gli altri pivot sono via via individuati come gli elementi che stanno sulla diagonale principale. In generale, per annullare tutti gli elementi della colonna sottostanti un pivot a_kk, si effettua la seguente operazione, valida per ogni i > j:

In pratica, a tutti gli elementi di una riga i si sostituiscono i rispettivi elementi individuati dalla combinazione lineare sopra descritta, rispetto alla riga contenente il pivot. Se per esempio si ha il sistema di equazioni

e quindi la corrispondente matrice:

per rendere nulli gli elementi della prima colonna, tranne il primo, si fa riferimento all’elemento a₁₁, che diventa il pivot e si operano le seguenti operazioni tra righe:

• r[2] ← r[2] − r[1] ⋅ 3

• r[3] ← r[3] − r[1]

La matrice del sistema è ora trasformata nella seguente:

Il pivot diventa ora l’elemento a₂₂ e si effettua la sostituzione:

La matrice del sistema è ora la seguente:

Risolvendo il sistema equivalente

si ha la soluzione