ortottica
Matematica
In geometria, caso particolare dell’isottica. O. di una curva piana assegnata è il luogo dei vertici di un angolo retto che varia in modo che i suoi lati rimangano tangenti alla curva data; in altri termini, è il luogo dei punti dai quali una porzione della curva (quella compresa fra i punti di contatto delle due tangenti per il punto) è vista sotto angolo retto.
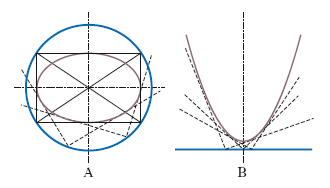
L’o. di un’ellisse è la circonferenza che passa per i vertici del rettangolo circoscritto all’ellisse (fig. A). L’o. di una parabola si riduce alla direttrice (fig. B). Analogamente, o. di due curve è il luogo descritto dai vertici di un angolo retto i cui lati variano restando rispettivamente tangenti alle due curve.
Medicina
Branca dell’oculistica che mira a rieducare la visione binoculare attraverso la correzione di deficit funzionali (per es., strabismo), mediante particolari esercizi e anche con l’ausilio di lenti.