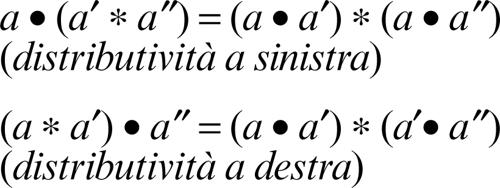operazione
operazione
operazione nel suo significato più elementare è una legge che a ogni coppia ordinata (a, b) di elementi di un insieme A associa un elemento di A. Tali sono le ordinarie operazioni di addizione e moltiplicazione dell’aritmetica (dove A è N, l’insieme dei numeri naturali). Il concetto si può generalizzare in più modi. Se A1, A2, ..., An sono n insiemi, un’operazione definita su di essi e a valori in un insieme B è una legge che associa a ogni elemento del prodotto cartesiano A1 × A2 × ... × An un elemento di B. Un’operazione è quindi un’applicazione ƒ: A1 × A2 × ... × An → B. Il numero degli n argomenti dell’applicazione ƒ (detti operandi) è detto arità dell’operazione e l’immagine b di un elemento (a1, a2, ..., an) del dominio è detto il risultato di a1, a2, ..., an. Un’operazione è detta unaria se la sua arità è 1 (questo è per esempio il caso dell’operazione di valore assoluto), è detta binaria se la sua arità è 2 (come l’addizione e la moltiplicazione), è detta ternaria se la sua arità è 3, ..., n-aria se la sua arità è n (per esempio è tale la media aritmetica di n numeri reali). Un’operazione binaria ∗: B × A → A in cui l’insieme A dei valori dell’operazione coincide con uno degli insiemi che compongono il dominio è detta anche una legge di composizione: più in particolare, essa è detta legge di composizione interna (o anche operazione binaria interna) se gli insiemi B e A coincidono, altrimenti è detta legge di composizione esterna (o anche operazione binaria esterna). Un importante esempio di legge di composizione esterna è la moltiplicazione per uno scalare in uno spazio vettoriale V definito su un campo K. Il caso più ricco è però quello delle leggi di composizione interne, vale a dire quello di un’operazione della forma ƒ: A × A → A. Se l’operazione è indicata con un simbolo operatorio ∗ (come per esempio +, ∘, ∙, ⋅, −, : ecc.), il risultato dell’operazione applicata a due elementi a, b è allora indicato mediante la notazione operatoria infissa a ∗ b, anziché quella funzionale ∗(a, b).
Proprietà delle operazioni
Una legge di composizione interna ∗ è detta commutativa se a ∗ a′ = a′ ∗ a per ogni a e a′ di A; associativa se (a ∗ a′) ∗ a″ = a ∗ (a′ ∗ a″) per ogni a, a′, a″ di A. Un elemento u di A è detto elemento neutro di ∗ se, per ogni a appartenente ad A, risulta a ∗ u = u ∗ a = a; un elemento z di A è detto invece elemento assorbente di ∗ se, per ogni a appartenente ad A, risulta a ∗ z = z ∗ a = z. Se esistono, l’elemento neutro e l’elemento assorbente di ∗, essi sono unici. Se ∗ è dotata di elemento neutro u, allora un elemento a di A è detto invertibile rispetto a ∗ se esiste un elemento b di A tale che a ∗ b = b ∗ a = u: se un tale elemento esiste, allora esso è unico ed è detto l’inverso di a. Se ogni elemento di A è invertibile rispetto a ∗, allora è possibile definire in A una seconda legge di composizione interna, detta operazione inversa di ∗: essa è definita come l’operazione ∗: A × A → A che associa alla coppia ordinata (a, b) l’elemento a ∗ b = a ∗ b–1, dove b−1 è l’inverso di b rispetto a ∗. Segue che un’operazione associativa ∗ e la sua operazione inversa ∗ sono legate dalle identità (b ∗ a) ∗ a = (b ∗ a) ∗ a = b, dove a e b sono arbitrari elementi di A. Ogni elemento di A è invertibile rispetto a ∗, e l’operazione inversa di ∗ coincide con l’operazione di partenza ∗. L’operazione inversa ∗ di un’operazione associativa e commutativa ∗ non è mai né associativa né commutativa; se però ∗ ammette elemento neutro allora anche ∗ ammette come elemento neutro lo stesso di ∗. Se ∙ e ∗ indicano due operazioni binarie interne su un insieme A, si dice allora che l’operazione ∙ è distributiva rispetto a ∗ se, per ogni a, a′, a″ di A, risulta
Se è definita l’operazione inversa ∗ di ∗ e se ∙ è distributiva rispetto a ∗, allora ∙ è distributiva anche rispetto a ∗. Un sottoinsieme A′ di A si dice chiuso rispetto all’operazione binaria interna ∗ se, per ogni coppia di elementi a, a′ di A′, il loro risultato a ∗ a′ è ancora in A′.
Insiemi e operazioni
Un insieme dotato di una o più operazioni binarie interne o esterne acquisisce una struttura algebrica; la particolare struttura algebrica di un insieme dipende dalle particolari proprietà soddisfatte dalle operazioni su di esso definite. Si può considerare più in particolare l’esempio offerto dall’insieme Z dei numeri interi. In esso si definiscono due operazioni binarie interne: l’addizione e la moltiplicazione. L’addizione è un’operazione associativa e commutativa; essa ha per elemento neutro 0 e ogni elemento è invertibile rispetto a essa: due elementi inversi rispetto all’addizione sono detti opposti. Dunque è ben definita in Z anche l’operazione inversa dell’addizione: tale è la sottrazione. Anche la moltiplicazione è un’operazione associativa e commutativa ed è distributiva rispetto alla addizione; essa ammette 1 per elemento neutro e ammette 0 per elemento assorbente. Nessun elemento diverso da 1 e −1 è invertibile rispetto alla moltiplicazione; pertanto essa non ammette operazione inversa. È possibile definire un’operazione inversa della moltiplicazione a patto di ampliare l’insieme Z all’insieme Q dei numeri razionali e di escludere lo 0: si ottiene in questo modo l’operazione di divisione. Restando nell’ambito dei numeri interi, si può però ricorrere all’operazione di divisione con resto, che approssima la divisione ai numeri interi: i risultati di tali operazioni coincidono se e solo se il divisore divide il dividendo, vale a dire se e solo se il risultato della divisione è un numero intero.