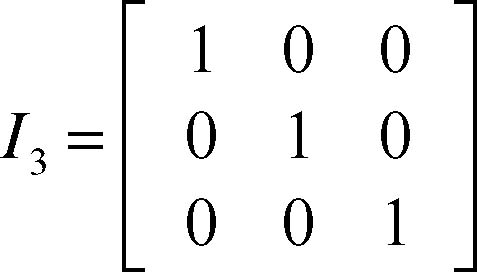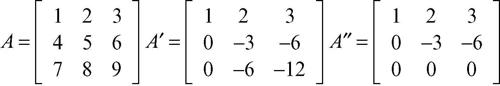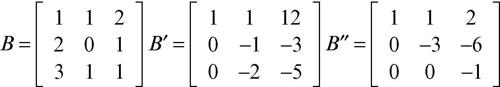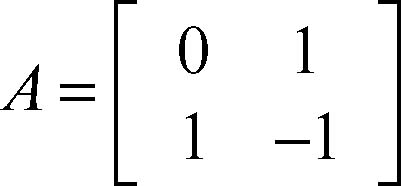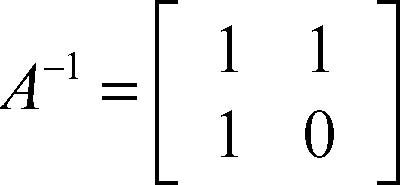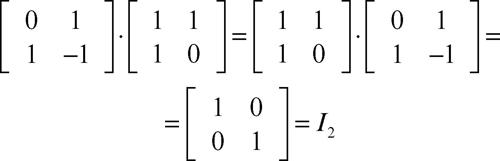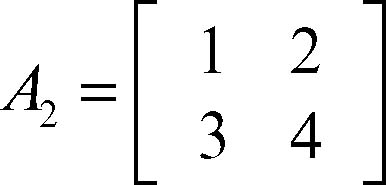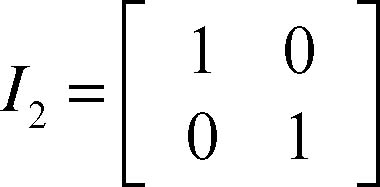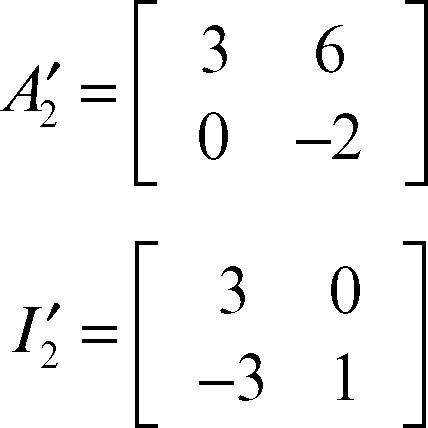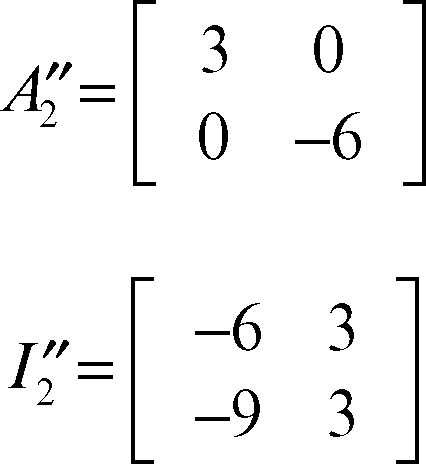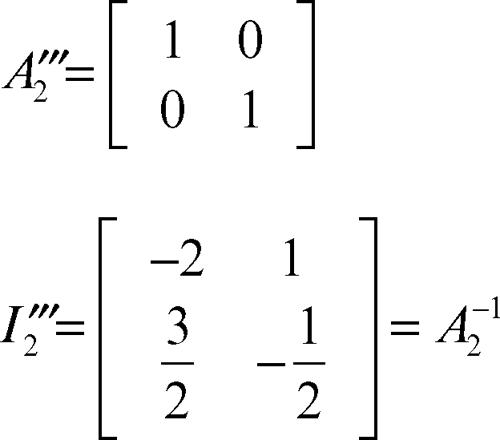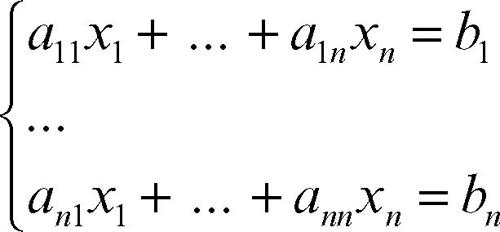matrice

matrice

matrice tabella rettangolare di simboli, detti elementi della matrice, che rappresentano numeri reali, numeri complessi o, più in generale, elementi di un campo K o di un anello A. Gli elementi della matrice sono disposti per righe e per colonne e ciascuno di essi è munito di due indici che corrispondono, nell’ordine, alla riga e alla colonna di appartenenza. In tal modo l’elemento che si trova sulla i-sima riga e sulla j-sima colonna è indicato con a_ij. Una matrice A con m righe e con n colonne è detta matrice m × n (a valori nel campo K o nell’anello A) ed è rappresentata come segue

oppure A = (a_ij), con i = 1, 2, ..., m e j = 1, 2, ..., n; è indicata anche con A_mn. Gli elementi si leggono: «a con uno uno, a con uno due, ... a con emme enne». Due matrici m × n sono uguali se sono ordinatamente uguali tutti gli elementi che occupano lo stesso posto. Se m = n, la matrice A è detta matrice quadrata ed è indicata anche con A_n. Il numero n delle righe o colonne di una matrice quadrata è detto ordine della matrice quadrata; gli elementi di indice i = j, cioè aventi indici uguali, formano la diagonale principale. Se m = 1, la matrice si riduce a una sola riga ed è detta matrice (o vettore) riga, se n = 1 si riduce a una sola colonna ed è detta matrice (o vettore) colonna. La matrice A^T, ottenuta dalla matrice A scambiando le righe con le colonne, è detta matrice trasposta di A. In campo complesso, la matrice A̅, ottenuta da A sostituendo ai suoi elementi i rispettivi numeri complessi coniugati, è detta matrice coniugata di A. Se la matrice ha tutti gli elementi reali coincide con la propria coniugata. Con la scrittura A̅^T si indica la matrice trasposta coniugata della matrice A (ottenuta, quindi, scambiando le righe con le colonne della matrice A e sostituendo ai suoi elementi i rispettivi complessi coniugati); la matrice trasposta coniugata è anche indicata a volte con A* o A^H.

Una matrice quadrata A_n è detta:

• matrice simmetrica se a_ij = a_ji per ogni i e j, se invece si ha a_ij = −a_ji è detta matrice antisimmetrica. Una matrice simmetrica coincide con la sua trasposta;

• matrice triangolare superiore se a_ij = 0 per i > j, cioè se gli elementi al di sotto della diagonale principale sono tutti nulli. Una tale matrice è anche detta matrice a scalini;

• matrice triangolare inferiore se a_ij = 0 per i < j, cioè se gli elementi al di sopra della diagonale principale sono tutti nulli;

• matrice diagonale se a_ij = 0 per i ≠ j cioè se gli elementi che non si trovano sulla diagonale principale sono tutti nulli;

• matrice quasi triangolare se elementi non nulli si trovano anche sulla codiagonale adiacente (la linea adiacente alla diagonale principale);

• matrice a banda di larghezza 2m + 1 se sono nulli tutti gli elementi al di fuori della diagonale principale e delle m codiagonali adiacenti: in particolare, per m = 1 la matrice si dice tridiagonale;

• matrice emisimmetrica se gli elementi aventi indici uguali ma in ordine diverso sono uguali in valore assoluto ma di segno opposto, cioè a_ij = −a_ji; nel caso di i = j deve essere a_ii = 0 (cioè gli elementi della diagonale principale di una matrice emisimmetrica sono tutti nulli).

Una matrice si dice sparsa se possiede una bassa percentuale di elementi non nulli (dell’ordine di 1 ogni n).

Una matrice diagonale i cui elementi sono tutti uguali a 1 è detta matrice unità o matrice identica ed è indicata con I_n. Per esempio, la matrice identica di ordine 3 sul campo dei reali è la matrice

• matrice unitaria se è una matrice a elementi complessi la cui inversa coincide con la trasposta coniugata.

Matrici equivalenti per righe o per colonne

Data una matrice A_mn, si chiamano operazioni elementari sulle righe di A_mn le seguenti operazioni:

• scambio di due righe;

• moltiplicazione di una riga per uno scalare diverso da zero;

• sostituzione di una riga con una combinazione lineare di altre righe.

Due matrici A_mn e B_mn si dicono matrici equivalenti per righe se è possibile passare dall’una all’altra mediante un numero finito di operazioni elementari sulle righe. In modo del tutto analogo si definiscono le operazioni elementari sulle colonne e l’equivalenza di due matrici per colonne. L’equivalenza per righe o per colonne è una relazione di equivalenza. Utilizzando le operazioni elementari, si ottengono, per esempio, le seguenti catene di matrici equivalenti:

La matrice A è equivalente a una matrice a due scalini, la matrice B è equivalente a una matrice a tre scalini. In generale una matrice A_mn è equivalente a una matrice a scalini il cui numero di scalini può essere al massimo il minore tra m e n. Interpretando le righe di una matrice come vettori, il numero di scalini della sua equivalente a scalini rappresenta il numero dei vettori riga indipendenti.

Operazioni tra matrici

Nell’insieme delle matrici è possibile introdurre operazioni di addizione e moltiplicazione.

• Addizione di matrici: se A = (a_ij) e B = (a_ij) sono due matrici m × n a elementi in un anello, la matrice C = A + B = (c_ij) tale che c_ij = a_ij + b_ij è detta matrice somma di A e B: è la matrice in cui ogni elemento è la somma degli elementi di ugual posto in A e B. Analogamente è definita la differenza tra matrici.

• Moltiplicazione di una matrice per uno scalare: se A = (a_ij) e k (scalare) è un elemento del campo al quale appartengono gli elementi di A, il prodotto k ⋅ A è una matrice C = (c_ij) tale che c_ij = k ⋅ a_ij per ogni i, j. Se k = −1 la matrice ottenuta, indicata con −A, si dice matrice opposta di A. La somma di una matrice con la sua opposta dà la matrice nulla, cioè la matrice i cui elementi sono tutti nulli. La matrice nulla è l’elemento neutro nell’operazione di addizione tra matrici.

• Moltiplicazione di matrici. Questa operazione è definita solo se il numero di colonne della prima matrice della moltiplicazione è uguale al numero di righe della seconda: è dunque sempre definita tra matrici quadrate dello stesso ordine sul campo dei numeri reali o complessi. L’operazione è anche chiamata moltiplicazione righe per colonne e dà per risultato una matrice avente tante righe quante ne ha la prima e tante colonne quante ne ha la seconda. Date per esempio le matrici A_mn e B_np, la matrice prodotto C_mp = A_mn ⋅ B_np ha come elemento di posto (i, j) il prodotto scalare della i–sima riga di A_mn con la j–sima colonna di B_np. L’operazione non è commutativa.

• Potenza di una matrice quadrata A con esponente intero positivo k è il prodotto di k fattori tutti uguali ad A: per essa valgono le usuali proprietà delle potenze.

La matrice identica funge da elemento neutro nella moltiplicazione di matrici quadrate dello stesso ordine. Le operazioni di addizione e moltiplicazione di matrici sui reali soddisfano le proprietà formali dell’addizione e moltiplicazione tra numeri interi, fatta eccezione per la proprietà commutativa della moltiplicazione e la legge di annullamento del prodotto (il prodotto A ⋅ B può infatti essere uguale alla matrice nulla senza che né A né B siano nulle).

L’insieme delle matrici m × n, con elementi in un campo K, con le operazioni di addizione e di moltiplicazione per uno scalare, forma uno spazio vettoriale.

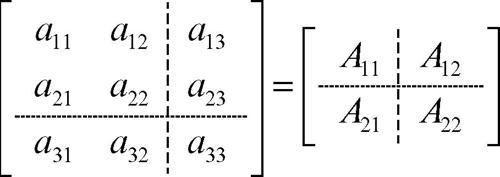
In alcuni casi è conveniente suddividere una matrice in sottomatrici (o blocchi), per esempio

sono matrici (ripartite) a blocchi, cioè matrici aventi per elementi matrici. Le operazioni su di esse si svolgono come quando gli elementi sono scalari. Una matrice quadrata si dice riducibile se può essere trasformata in modo equivalente in una matrice della forma che compare alla destra dell’uguaglianza in (1), con A₁₁ e A₂₂ quadrate e A₂₁ nulla.

Determinante e rango di una matrice

A ogni matrice quadrata A con elementi reali si associa un numero reale detto → determinante e indicato con det(A), detA o anche con |A|. Una matrice quadrata si dice singolare se ha determinante nullo. Si dice rango o caratteristica di una matrice A_mn, e si indica con r(A_mn) o semplicemente r, l’ordine massimo dei minori non nulli estraibili da essa (→ Kronecker, teorema di), cioè delle sottomatrici quadrate a determinante non nullo ottenute considerando gli elementi comuni a k righe e k colonne. Il rango è importante nella soluzione di sistemi lineari m × n e nello studio delle applicazioni lineari tra spazi vettoriali. Il rango r fornisce il numero dei vettori riga (o colonna) linearmente indipendenti.

Matrice inversa

Se A è una matrice quadrata di ordine n con elementi appartenenti a un campo e detA ≠ 0, allora esiste ed è unica la matrice quadrata A⁻¹, dello stesso ordine di A, detta matrice inversa di A, tale che A ⋅ A⁻¹ = A⁻¹ ⋅ A = I_n; in altri termini la matrice inversa è la matrice che moltiplicata per A dà come risultato la matrice identità dello stesso ordine. Una matrice dotata di inversa è detta anche matrice invertibile e condizione necessaria e sufficiente affinché lo sia è che il suo determinante sia diverso da zero. Per esempio, per la matrice

risulta detA = −1 ≠ 0 e la sua inversa è la matrice

Si ha infatti:

L’insieme delle matrici quadrate invertibili di ordine n, con elementi appartenenti a un campo K, è detto gruppo lineare generale, è indicato con il simbolo GL(n, K) e risulta isomorfo al gruppo degli automorfismi di uno spazio vettoriale di dimensione n sul campo K.

In generale, l’inversa di una matrice quadrata A_n non singolare è la matrice A_n⁻¹ = (b_ij) dove l’elemento di posto (i, j) è così calcolato:

Il simbolo A_ji indica qui l’aggiunto in A dell’elemento a_ji, cioè la matrice ottenuta da A eliminando la j-esima riga e la i-esima colonna.

Algoritmo di Gauss-Jordan per determinare la matrice inversa

Oltre alla precedente procedura, che richiede in generale molti calcoli, è possibile determinare l’inversa di una matrice quadrata non singolare con metodi più semplici quali, per esempio, l’algoritmo di Gauss-Jordan, che deriva dal metodo di → Gauss per la risoluzione dei sistemi lineari. Data una matrice quadrata A_n non singolare, si possono infatti applicare a essa i successivi passi del metodo di Gauss fino a ridurla, prima, a una matrice triangolare, poi a una matrice diagonale e infine a una identica I_n. Compiendo gli stessi passi a partire dalla matrice identica I_n si perviene a una matrice che risulta essere l’inversa di A_n. Per esempio, data la matrice

si compiono i seguenti passi di Gauss su essa come sulla matrice

In ognuna delle due matrici si moltiplica la prima riga per 3 e alla seconda riga si sottrae la prima:

Si moltiplica la seconda riga per 3 e la si addiziona alla prima riga:

Infine, si divide la prima riga per 3 e la seconda riga per −6 in modo che la matrice A₂ si trasformi nella matrice identica:

L’ultima matrice ottenuta è proprio l’inversa della matrice data A_2.

==Matrice inversa generalizzata==

Se A è una matrice m × n qualunque, si chiama inversa generalizzata di A, e si indica con A⁻ ogni matrice n × m tale che A ⋅ A⁻ ⋅ A = A; si chiama pseudoinversa di A, e si indica con A⁺, l’unica matrice che, oltre alla proprietà precedente, soddisfa anche le tre seguenti:

Matrice ortogonale

Una matrice A la cui trasposta coincide con la sua inversa è detta matrice ortogonale e rappresenta una isometria. Ogni matrice ortogonale può essere considerata come matrice del cambiamento di base tra due basi ortonormali. Il determinante di una matrice ortogonale è 1 oppure −1.

Il calcolo matriciale e le sue applicazioni

Lo studio sistematico delle operazioni sulle matrici e delle loro proprietà costituisce l’oggetto del calcolo matriciale. La notazione e il calcolo matriciali sono utilizzati in molti rami della matematica, poiché consentono di esprimere in forma compatta alcune proprietà, ovvero di eseguire certi calcoli che in altre forme risulterebbero assai gravosi. Per esempio, un sistema di n equazioni algebriche lineari in n incognite

si può scrivere in forma compatta A ⋅ X = B, quando si sia definita la matrice dei coefficienti in modo naturale come A = (a_ij), e X, B siano matrici colonna costituite rispettivamente dalle incognite e dai termini noti. Se A è non singolare, moltiplicando a sinistra per A⁻¹ si trova direttamente X = A⁻¹ ⋅ B; questa espressione, che riassume la cosiddetta formula di Cramer, richiama la formula risolutiva x = a⁻¹b = b /a dell’equazione in una variabile ax = b: alla condizione a ≠ 0, necessaria e sufficiente per l’esistenza di un’unica soluzione, corrisponde, nel caso del sistema, la condizione |A| ≠ 0.

Le matrici in ambito informatico

In informatica, una matrice è una struttura multidimensionale di dati dello stesso tipo ed è più propriamente detta → array. Nella maggior parte dei linguaggi di programmazione è possibile definire un array e fare riferimento ai dati in esso contenuti tramite nome e indice. Un testo è un esempio di array monodimensionale, dove ogni carattere è un elemento e il suo indice è la posizione che occupa nel testo stesso. Una bitmap è un esempio di array bidimensionale: ogni pixel è individuato dalla posizione nella riga e nella colonna (si veda → grafica computerizzata).