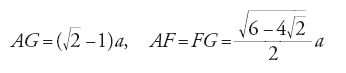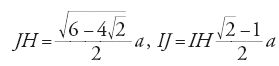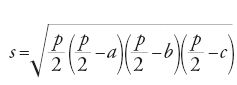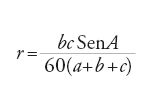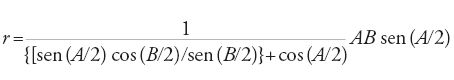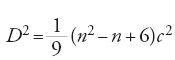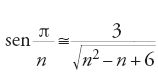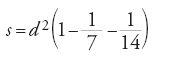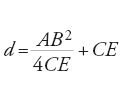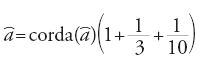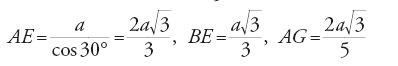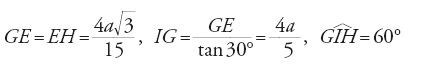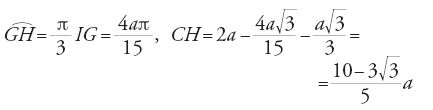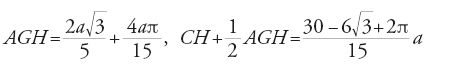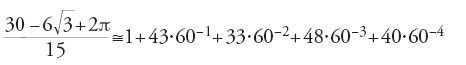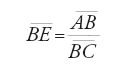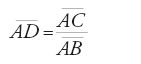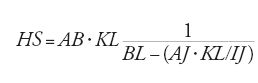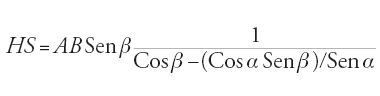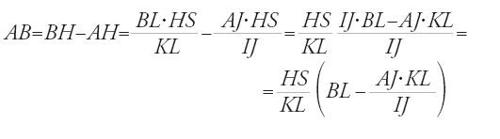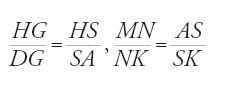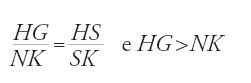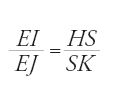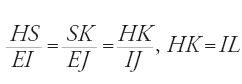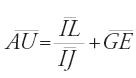La civiltà islamica: antiche e nuove tradizioni in matematica. Geometria pratica
La civilta islamica: antiche e nuove tradizioni in matematica. Geometria pratica
Geometria pratica
Nella classificazione delle scienze di al-Fārābī figura la categoria dei 'procedimenti ingegnosi' (῾ilm al-ḥiyal) che comprende tra l'altro l'algebra assieme a un complesso di discipline, nelle quali si mescolano scienze matematiche ed elementi materiali, a dimostrazione che a quel tempo (X sec.) i confini tra sapere e fare tracciati da un certo aristotelismo non erano più molto rigidi. L'attenuazione di questa opposizione si incontra anche in un teorico della dimostrazione in geometria come Ibn Sinān, secondo il quale per quanto riguarda la dimostrazione non c'è più ragione di distinguere tra costruire e dimostrare. L'applicazione della matematica si vede allora attribuire un vero e proprio status. In questa categoria della scienza dei procedimenti ingegnosi entrano trattati sulle costruzioni geometriche assieme a trattati di arte della misura. Tuttavia, se fin dalla più lontana antichità si incontrano qua e là formule pratiche di calcolo di aree o di volumi (esatte, approssimate o anche decisamente errate) e vari procedimenti di costruzione, è a partire dal X sec. e nel mondo arabo che la geometria pratica come scienza dei procedimenti ingegnosi acquista dignità di disciplina, aprendo ai matematici un nuovo campo di attività in margine alla geometria euclidea.
I trattati di geometria pratica non sono opere didattiche rivolte a futuri matematici e rientrano in una tradizione, risalente alla fine del IX sec., di opere scritte da matematici a beneficio di un pubblico di non specialisti. Il loro studio è al crocevia della storia della scienza e della tecnica, ma anche della storia dell'arte e della società. I trattati sono di vario tipo, a seconda del pubblico cui si rivolgono e che esprime bisogni, culture e sensibilità diverse: artigiani, geometri, ingegneri, architetti, fabbricanti di strumenti astronomici, impiegati amministrativi (kuttāb), ecc. Per via di questa diversità di pubblico il livello teorico è molto vario: alcuni non contengono dimostrazioni, altri soltanto un abbozzo, altri ancora riportano qualche dimostrazione particolareggiata, rimandando per altre agli Elementi di Euclide o alle opere di Archimede.
Essi possono essere raggruppati in tre grandi generi:
1) trattati sulle misure ottiche nel solco dell'Ottica di Euclide. Iniziati da al-Kindī (IX sec.) nell'opera Fī taqwīm al-ḫaṭa᾽ wa-'l-muškilāt allatī li-Uqlīdis fī 'l-Manāẓir (Sulla rettifica degli errori e delle difficoltà riscontrabili nell'Ottica di Euclide), sono studi di stereometria che saranno proseguiti da Sinān ibn al-Fatḥ (IX sec.), al-Qabīṣī (X sec.) e infine da Ibn al-Hayṯam (XI sec.);
2) capitoli sulle misurazioni, parti di opere di ḥisāb (scienza del calcolo) nel solco della seconda parte dell'opera di al-Ḫwārizmī. Trattati di questo tipo sono numerosissimi; ricordiamo a titolo di esempio soltanto quelli di al-Karaǧī (X sec.), di al-Fārisī (665-719/1267-1319) e di al-Kāšī (m. 832/1429); Miftāḥ al-ḥisāb (La chiave del calcolo), ancora di al-Kāšī, è in un certo senso il punto d'arrivo di tale tradizione;
3) trattati sulle costruzioni geometriche rivolti agli artigiani; in questi figurano scritti sulla costruzione di strumenti astronomici studiati nella parte di quest'opera dedicata all'astronomia e sui quali non ritorneremo.
Le costruzioni geometriche a uso degli artigiani
Non era raro nel X sec. che artigiani e geometri dibattessero questioni di geometria pratica, una collaborazione di cui purtroppo ci sono pervenute poche testimonianze scritte. Uno dei primi trattati andati perduti è forse quello sulla costruzione di quadranti solari (strumenti delle ombre), del matematico Ibn Sinān della prima metà del X secolo; lo avrebbe dettato, senza dimostrazioni, a un fabbricante di strumenti astronomici:
Avevo fatto, in termini diversi da quelli utilizzati nel mio libro, un lavoro che avevo dato a un certo artigiano. In realtà questi aveva costruito per noi un'armilla […]. Ho ammirato la sua arte, e costatato che applicava procedimenti sottili nelle sue opere, gli ho dettato allora le caratteristiche dello strumento […] ho fatto in modo che la caratterizzazione fatta per lui andasse bene per artigiani che lavorano a mano mentre nel mio libro ho fatto in modo che questa determinazione avvenisse per mezzo dell'analisi […]. Se accade che qualcuno vede una differenza tra [questo libro] e i tre capitoli, ecco spiegato il perché. (Rashed 2000b, p. 10)
Abū 'l-Wafā᾽ al-Būzǧānī (328-388/940-998) nel trattato Fī mā yaḥtāǧu al-ṣāni῾ min al-a῾māl al-handasiyya (Sulle costruzioni geometriche indispensabili all'artigiano) fa anch'egli allusione a questa collaborazione tra artigiani e geometri, sottolineando le differenze di atteggiamento degli uni e degli altri di fronte ai problemi dibattuti: mancanza di senso pratico da parte dei geometri, mancanza di conoscenze di carattere teorico per quanto riguarda gli artigiani. Faremo riferimento soprattutto a questo trattato, uno dei rari pervenuti sull'argomento. Al-Būzǧānī è un matematico eminente e il suo al-Maǧisṭī uno dei testi di fondazione della trigonometria. Non disdegnava di occuparsi di problemi pratici: oltre al trattato Fī mā yaḥtāǧu al-ṣāni῾ min al-a῾māl al-handasiyya è anche autore di un libro di aritmetica pratica a uso dei funzionari dello Stato (kuttāb). Del Fī mā yaḥtāǧu al-ṣāni῾ abbiamo una versione araba e un'antica versione persiana. Questo testo è stato commentato in arabo da Kamāl al-Dīn ibn Yūnus (XII sec.), e in persiano da al-Yazdī (XVI sec.), e ciò può essere indice di una certa diffusione anche negli ambienti di lingua persiana: è nota infatti l'importanza delle figure geometriche come elemento decorativo nell'arte e nell'architettura islamica (arabeschi e ornamenti a intreccio su pavimentazioni a mosaico o pannelli di legno scolpito o incrostati, decorazioni di cupole, e così via).
Nel primo capitolo del trattato, al-Būzǧānī descrive gli strumenti che l'artigiano utilizza. Innanzi tutto la riga per i disegni e i tratti brevi, perché le rette più lunghe venivano tracciate servendosi di una cordicella tesa rivestita di una patina di nero; mostra poi come verificare se una riga è dritta, sia a occhio sia rivoltandola e verificando che i due tracciati ottenuti si sovrappongono. Seguono il compasso (eventualmente dotato di un dado per fissarne l'apertura) e il compasso a ruota per tracciare grandi cerchi; quindi la squadra, per la quale indica diversi modi di costruzione e di verifica, basati sulla costruzione dell'asse di un segmento con la riga e il compasso, sul fatto che il centro del cerchio circoscritto a un triangolo rettangolo è il punto di mezzo dell'ipotenusa, o che la mediana è la metà dell'ipotenusa. Tra tali metodi, quello che egli attribuisce agli artigiani e che sembra essere stato in uso fin dall'Antichità, si basa sul teorema di Pitagora (si traccia con il compasso un segmento lungo 3 unità su un lato della squadra, uno lungo 4 sull'altro lato e si verifica che la retta che unisce gli estremi sia lunga 5); ritroveremo questo metodo di verifica della perpendicolarità basato sul calcolo in tutti i trattati di geometria pratica. Al-Būzǧānī non parla di strumenti di misura degli angoli (goniometri, astrolabi, ecc.); in un trattato più tardo, Kitāb fī ma῾rifat al-ḥiyal al-handasiyya (Libro della conoscenza dei procedimenti ingegnosi) di Ismā῾īl ibn al-Razzāz al-Ǧazarī, dei primi del XIII sec., vi è la descrizione di uno strumento costituito da una riga mobile rotante su una riga fissa, sulla quale è fissato un semicerchio graduato, strumento che permette, come un goniometro, di tracciare un angolo di una data misura in gradi.
Al-Būzǧānī indica poi diverse costruzioni che intervengono in molti problemi, dai più semplici (bisecare un segmento, un arco o un angolo, abbassare una perpendicolare a una retta, trisecare un segmento, costruire un angolo o un triangolo uguale a uno assegnato, tracciare una parallela a una retta data, determinare il centro di un cerchio ‒ inscrivendo in questo cerchio un triangolo rettangolo ‒, tracciare una tangente a un cerchio da un punto dato), ai meno semplici (abbassare una perpendicolare su un piano non orizzontale, altrimenti si utilizza il filo a piombo), fino ai più complicati (trisecare un angolo, duplicare un cubo, costruire una parabola).
La trisezione dell'angolo
Per la trisezione di un angolo diverso dall'angolo retto, impossibile con riga e compasso, egli dà due neũsis delle quali conserva solo l'aspetto pratico. Queste permettono effettivamente a un artigiano di tracciare semplicemente e con un'eccellente approssimazione la retta cercata. La prima neusis è quella risolta e dimostrata alla fine del trattato dei Banū Mūsā, Kitāb Ma῾rifat misāḥat al-aškāl al-basīṭa wa-'l-kuriyya (Libro per conoscere l'area delle figure piane e sferiche), e che si basa su un arco di concoide di cerchio.
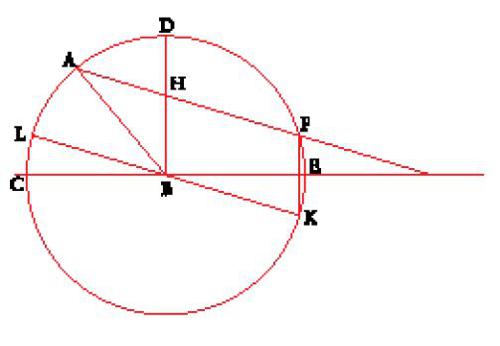
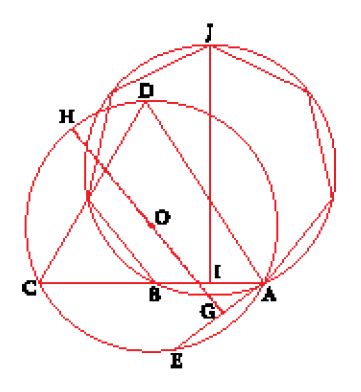
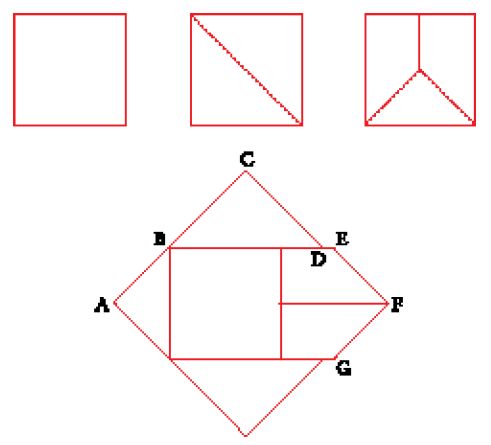
Supponiamo che l'angolo da trisecare sia l'angolo ABC e che sia acuto (fig. 2). Si traccia un cerchio CAD di centro B e la retta BD ortogonale a BC, si fa ruotare attorno al punto A una riga mobile AHF che interseca BD in H e il cerchio CAD in F finché HF=BD. Sia E il punto diametralmente opposto a C, K il punto simmetrico di F rispetto a E. BK incontra il cerchio in L e LBC=(1/3)ABC.
Nella costruzione esposta da al-Būzǧānī le costruzioni ausiliarie che servivano a dimostrare la neũsis sono scomparse e altre costruzioni sono rese più semplici (non si costruisce più BK parallela a HF, ma si prende K simmetrico di F rispetto ad E).
La seconda neũsis si trova risolta (mediante un'iperbole) nel testo Qismat al-zāwiya bi-ṯalāṯat aqsām mutasāwiya (Divisione dell'angolo in tre parti uguali) di Ṯābit ibn Qurra.
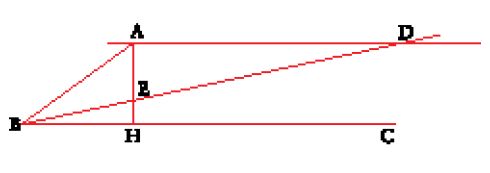
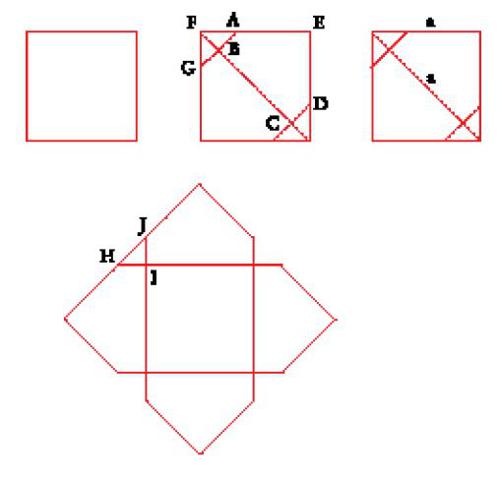
Supponiamo che ABC sia l'angolo da trisecare e che sia acuto (fig. 3). Si abbassa la perpendicolare AH su BC, si traccia la parallela AD a BC e si fa ruotare attorno al punto B una riga mobile che interseca AD e AH rispettivamente in D ed E finché DE=2AB; allora DBC=(1/3)ABC.
La duplicazione del cubo
Per la duplicazione del cubo, altro problema non risolubile con riga e compasso, al-Būzǧānī indica ancora una neũsis, quella che Erone di Alessandria espone nella Mechanica, tradotta in arabo da Qusṭā ibn Lūqā nel IX secolo. Questa neũsis si basa sull'intersezione di un cerchio e di un'iperbole, ed equivale a una delle soluzioni di questo problema esposte e dimostrate da al-Ḫāzin nella prima metà del X secolo.
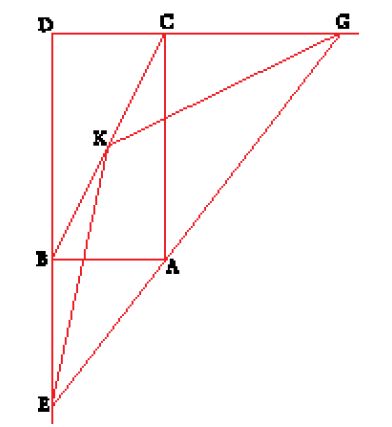
Sia AB il lato del cubo che si vuole duplicare (fig. 4). Si costruisca il rettangolo ABDC di centro K tale che BD=2AB e si prolunghino il lati DC e DB. Una riga mobile rotante attorno al punto A interseca DB in E e DC in G in modo che KG=KE; allora BE3=2AB3 e BE è il lato del cubo cercato.
Questi metodi di risoluzione per neũsis di problemi non risolubili con riga e compasso ereditati dall'antica Grecia, saranno progressivamente abbandonati dai geometri a partire dal X sec., a vantaggio di metodi di risoluzione di equazioni di terzo grado per intersezione di coniche. Tuttavia l'interesse pratico per gli artigiani resta, perché essi permettono di costruire con semplicità e con un'eccellente approssimazione le linee cercate.
Gli specchi ustori
Per la costruzione di specchi ustori, problema che a partire da al-Kindī suscitò un grande interesse nel mondo arabo, il testo di al-Būzǧānī è uno dei rari esemplari che ci sono pervenuti dopo quello di al-Kindī e prima della trasformazione operata da Ibn Sahl. Al-Būzǧānī espone senza dimostrazioni due metodi di costruzione per punti di una parabola. Il primo, che permette di costruire soltanto quei punti della parabola tali che la distanza dal vertice della loro proiezione ortogonale sull'asse non supera la metà del lato retto, è un metodo originale che a giudizio di Roshdi Rashed (Neugebauer 1999) potrebbe derivare da procedimenti proiettivi utilizzati nella stessa epoca da alcuni contemporanei come al-Qūhī.
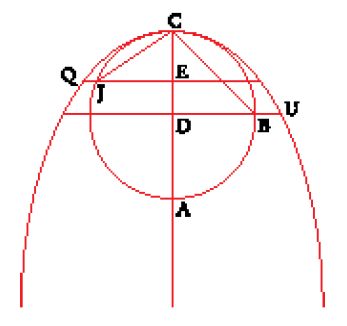
Sia dato un cerchio di centro D e diametro CA uguale al lato retto della parabola cercata di vertice C. Per tutti i punti E di CD si costruisca il punto Q tale che EQ=CJ. Il punto Q appartiene allora alla parabola di asse CA, vertice C e lato retto AC. Infatti: EJ2=EC∙EA, EQ2=CJ2=EJ2+EC2=EC∙EA++EC2=CE∙CA.
Il secondo metodo, che permette di costruire un arco qualunque di parabola è quello che si trova nel trattato di Ibrāhīm ibn Sinān Fī rasm al-quṭū῾ al-ṯalāṯa (Sul tracciato delle tre sezioni coniche).
Al-Būzǧānī si dilunga sui particolari della realizzazione pratica di uno specchio: costruzione di un modello con uno o l'altro dei metodi precedenti, rettifica di questo modello, formatura dello specchio sul modello in una sostanza riflettente (ferro, rame o carbonato di piombo), levigatura dello specchio con una lima che ha la stessa curvatura del modello. Ciò lascia pensare che probabilmente questi specchi, anche se non vi sono resti archeologici, siano stati effettivamente costruiti.
I poligoni regolari: costruzione dell'ettagono
Al-Būzǧānī affronta poi la costruzione di poligoni regolari (triangoli, quadrati, pentagoni, esagoni, ettagoni, ottagoni, ennagoni, decagoni) di lato assegnato o inscritti in un cerchio dato, figure di cui è nota l'importanza come elementi decorativi (arabeschi e ornamenti a intreccio) o architettonici (mausolei ottagonali del Cairo, mausolei o minareti su piani di ottagoni stellati in Iran o in Afghanistan). Egli mette in guardia contro il metodo, che giudica troppo grezzo, in uso presso certi artigiani, i quali per costruire un poligono regolare inscritto in un cerchio procedono per tentativi successivi con un compasso (e non suggerisce a questo proposito di usare l'equivalente di un goniometro). I poligoni regolari circoscritti a un cerchio sono poi costruiti a partire da poligoni inscritti, tracciando dai vertici di questi poligoni le tangenti al cerchio. Al-Būzǧānī presenta diverse costruzioni di alcuni di questi poligoni, alcune fatte con un compasso ad apertura fissa (quadrato, pentagono, ottagono, decagono).
Tra questi poligoni i soli non costruibili con riga e compasso sono l'ettagono e l'ennagono. Il problema dell'ennagono si risolve partendo dal triangolo equilatero e utilizzando la trisezione dell'angolo della quale abbiamo esposto il principio. Il problema dell'ettagono è stato oggetto, nel mondo arabo tra il IX e l'XI sec., di una vera e propria infatuazione tra i matematici più eminenti. Ne vengono date diverse costruzioni esatte basate sull'intersezione di coniche. Nei motivi decorativi o architettonici gli ettagoni regolari sono rari, ma al-Būzǧānī dà nondimeno due metodi di costruzione approssimata di questo poligono, che derivano dall'approssimazione data da Erone di Alessandria nei Metrica: se C è un cerchio di centro O nel quale è inscritto un esagono, allora il lato dell'ettagono inscritto nello stesso cerchio è approssimativamente uguale alla distanza di O da uno dei lati dell'esagono.
Il primo metodo di costruzione di un ettagono regolare di lato AB assegnato passa, come le costruzioni esatte date nello stesso periodo da Abū 'l-Ǧūd e da al-Siǧzī, per la costruzione di un triangolo isoscele di angolo al vertice π/7: siano C il simmetrico di A rispetto a B, D un punto tale che ACD sia un triangolo equilatero, E un punto del cerchio ACD tale che AE=AB (fig. 7). AB non è altro che la distanza del centro del cerchio ACD dal lato dell'esagono inscritto nel cerchio, cioè, con l'approssimazione di Erone, il lato dell'ettagono inscritto nello stesso cerchio. Sia G il punto di mezzo di AE; l'asse di AE interseca l'arco di circonferenza ADE (il più grande dei due) in H. Siano I il punto di mezzo di AB, J un punto dell'asse di AB tale che IJ=GH (i triangoli AHE e ABJ sono triangoli isosceli uguali di angolo al vertice approssimativamente uguale a π/7). Si traccia la circonferenza ABJ e si ottengono i vertici dell'ettagono riportando successivamente sulla circonferenza archi uguali ad AB a partire da A. Questo metodo permette di costruire con un'eccellente approssimazione un ettagono regolare perché equivale a prendere √3/(4+√13) come valore approssimato di tan(π/14), con un errore di 5∙10-4.
Il secondo metodo di costruzione di un ettagono regolare inscritto in un cerchio assegnato deriva più direttamente dall'approssimazione di Erone.
Sia C il cerchio assegnato di centro D e diametro AC (fig. 8). Il cerchio di centro A e raggio AD interseca C nei punti E e B (EA e AB sono due dei lati dell'esagono inscritto nel cerchio C). Sia G il punto di intersezione tra AC ed EB; il cerchio di centro B e raggio BG interseca C in H, e BH è un lato dell'ettagono (BG è una delle altezze del triangolo equilatero BAD e dunque è uguale alla distanza di D dal lato AB dell'esagono).
Figure inscritte o circoscritte ad altre
Al-Būzǧānī passa poi più in generale alla costruzione di figure inscritte o circoscritte a quadrati o a triangoli equilateri, che intervengono in diversi motivi di decorazioni, arabeschi o pavimentazioni.
Si tratta del triangolo equilatero inscritto in un quadrato (5 metodi), del quadrato circoscritto a un triangolo equilatero (fig. 9a), del triangolo equilatero circoscritto a un quadrato (fig. 9b), del quadrato circoscritto a un triangolo scaleno (il triangolo deve essere acutangolo, 3 metodi).
La costruzione di un quadrato inscritto in un triangolo scaleno fa intervenire implicitamente alcune omotetie, trasformazioni che si cominciano a utilizzare in opere di geometria nel X secolo.
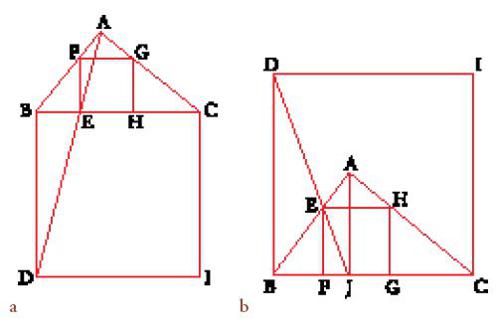
Sia ABC il triangolo assegnato, CBDI uno dei due quadrati costruiti sul lato BC (nel semipiano non contenente A (fig. 10a), o nel semipiano che contiene A (fig. 10b)). AD taglia BC in E, DJ (J è la proiezione ortogonale di A su BC) taglia AB in E.
Il primo metodo si basa sul fatto che l'omotetia di centro A che trasforma D in E trasforma il quadrato DBCI nel quadrato EFGH inscritto nel triangolo ABC, il secondo sul fatto che l'omotetia di centro J che trasforma D in E trasforma il quadrato DBCI nel quadrato EFGH.
Osserviamo che se al-Būzǧānī fa anch'egli uso di omotetie per costruire un triangolo equilatero circoscritto a un triangolo scaleno (fig. 11a), o un triangolo equilatero inscritto o circoscritto a un pentagono regolare (fig. 11b), non ne fa uso invece, anche se sarebbe stato possibile, per inscrivere un triangolo equilatero in un triangolo scaleno.
Dopo aver presentato metodi di costruzione di un rombo inscritto in un pentagono regolare e di un quadrato circoscritto a un pentagono regolare (quattro vertici del pentagono sono sui lati del quadrato, il quinto è all'interno del quadrato, sulla diagonale; fig. 12), che si basano sul fatto che l'asse di uno dei lati del pentagono è asse di simmetria della figura, al-Būzǧānī fa uso della seconda costruzione per risolvere il problema inverso, dell'inscrizione di un pentagono regolare in un quadrato (e ancora tale che quattro vertici del pentagono siano sui lati del quadrato e il quinto all'interno del quadrato, sulla diagonale). Sia ABCD un quadrato assegnato, IJKLM un pentagono di cui uno degli assi di simmetria è parallelo a una diagonale del quadrato; si costruisce con il metodo precedente un quadrato NOPQ circoscritto a IJKLM; l'omotetia che trasforma il quadrato NOPQ nel quadrato ABCD trasforma il pentagono IJKLM in un pentagono inscritto in ABCD.
Nella costruzione di al-Būzǧānī solamente quattro dei cinque vertici del pentagono sono sui lati del quadrato; non si tratta dunque della difficile proposizione di al-Qūhī, che costruisce un pentagono equilatero ma non equiangolo, nel quale i cinque vertici sono sui lati del quadrato per intersezione di due iperboli.
Al-Būzǧānī termina il capitolo con le costruzioni elementari di un ottagono inscritto in un quadrato e di un quadrato circoscritto a un ottagono.
Divisione delle figure e costruzione di poliedri regolari e semiregolari
Il capitolo che tratta della divisione delle figure (triangoli, quadrilateri, cerchi, figure limitate da un arco di cerchio e da due rette che formano un angolo assegnato) in parti aventi un rapporto assegnato riprende essenzialmente quanto si può trovare nel trattato di Euclide Divisioni delle figure. Il capitolo si conclude con costruzioni che mirano a suddividere alcuni terreni (quadrati, triangoli, trapezi) in modo da lasciare una via d'accesso di larghezza assegnata a due o tre porzioni di uguale superfice (queste costruzioni presentano lacune sulle quali ha attirato l'attenzione Franz Woepcke nel 1851).
Il trattato di al-Būzǧānī termina con la costruzione di poliedri regolari e semiregolari inscritti in una sfera. L'autore si propone di fornire metodi di costruzione di questi poliedri sulla superficie della sfera (senza far intervenire punti interni alla sfera), in modo tale che possano eventualmente essere utilizzati per decorare cupole. Osserviamo che egli non parla mai (e nemmeno Ibn al-Hayṯam nel trattato sulla misura) della possibilità di tracciare un cerchio massimo per due punti dati sulla sfera mediante l'uso di una cordicella tesa tra questi due punti.
Tassellature del piano
Il penultimo capitolo è dedicato a un problema che tra tutti quelli risolti da al-Būzǧānī in quest'opera sembra essere quello che riguarda più da vicino gli artigiani, per i quali è stato scritto. Si tratta infatti di costruire un quadrato a partire da quadrati e, viceversa, di decomporre un quadrato in quadrati. Questo problema si pone quando si vogliono costruire mosaici di pavimentazioni o pannelli di legno scolpito o incrostato: come per le muqarnas i moduli di base di questi elementi decorativi sono quasi sempre quadrati. I metodi esposti si potrebbero definire metodi di 'taglia e incolla', facilmente applicabili dagli artigiani. È in questo capitolo e a proposito di questi problemi che al-Būzǧānī parla di riunioni tra geometri e artigiani alle quali dice di aver assistito, come pure dei dibattiti suscitati da questi problemi.
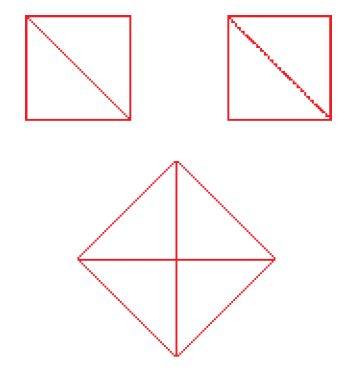
Egli risolve innanzi tutto il problema semplice di ricostruire un quadrato a partire da 2n2 quadrati uguali di lato a. La soluzione si basa sul fatto che la diagonale di un quadrato di lato na è uguale a na√2: si costruiscono due quadrati di lato na tagliati da una diagonale e si ricompongono in un quadrato (fig. 13).
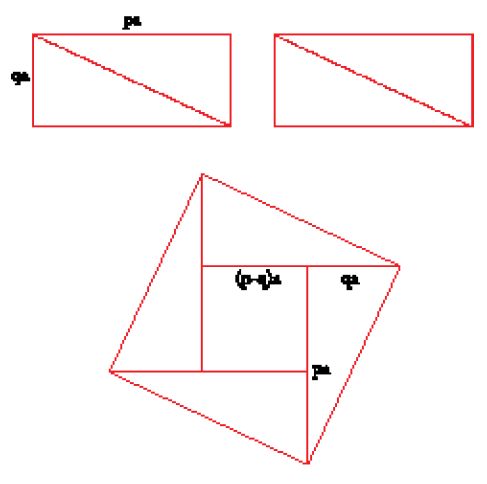
Al-Būzǧānī passa poi a costruire un quadrato a partire da p2+q2 quadrati uguali di lato a (p>q); la costruzione si basa sul fatto che p2+q2=(p−q)2+2pq. Si costruiscono un quadrato di lato (p−q)a e due rettangoli uguali di lati pa e qa, si tagliano a metà questi rettangoli con una diagonale e si ricostruisce un quadrato (fig. 14). Il procedimento si può invertire per decomporre un quadrato in p2+q2 quadrati uguali.
A proposito del problema "costruire un quadrato a partire da tre quadrati uguali di lato a", al-Būzǧānī espone due esempi di costruzioni non esatte effettuate da artigiani (i due metodi danno il risultato con la stessa approssimazione, che d'altra parte è abbastanza buona).
Primo metodo non esatto: si taglia uno dei quadrati con una diagonale, da un altro si separano un triangolo rettangolo isoscele di ipotenusa a e due trapezi rettangoli e si sovrappongono i pezzi (fig. 15).
A, B e C sono allineati, CDB+DEF=π e BCE=EFG=π/2, ma AB+BC=CD+EF=[1+(√2/2)]a (e non a√3), in quanto BD=a√2 e BE=[1+(1/2)]a. Vi è dunque una leggera sporgenza ED=[(3/2)−√2]a ∼0,086 a.
Secondo metodo non esatto: si tagliano due quadrati lungo le diagonali, si separano ai vertici alla base dei quattro triangoli rettangoli isosceli così ottenuti due piccoli triangoli rettangoli isosceli, in modo da lasciare un poligono ABCDE tale che BC=a, e si sovrappongono i pezzi (fig. 16).
Qui la difficoltà viene dal fatto che i triangoli rettangoli isosceli AFG e JIH non sono uguali perché
mentre
Vi è dunque una leggera sporgenza AF−IJ∼0,086 a.
Dopo aver criticato anche il metodo proposto dai geometri (che si basa sulla costruzione ben nota di √3 con riga e compasso, senza interesse pratico per risolvere il problema posto) al-Būzǧānī espone il proprio metodo: si tagliano due dei quadrati con le diagonali e si dispongono opportunamente i quattro triangoli così ottenuti (fig. 17). Si ha BC=FG=a, CFG=BCF=π/4; BCGF è dunque un parallelogramma, CF e BG si intersecano nel loro punto di mezzo M e i triangoli BCM e GFM sono uguali. Basta allora tagliare il triangolo BCM e porlo in GFM, e fare lo stesso con gli altri triangoli.
Al-Būzǧānī espone infine un procedimento che permette di formare un quadrato da due quadrati di dimensioni diverse (di lati a e b, con a>b), procedimento che permette, almeno teoricamente, di formare per iterazione un quadrato a partire da n quadrati di dimensioni diverse. Si basa sul fatto che a2=(a−b)2+ab+b(a−b); il principio di costruzione è lo stesso che permette di costruire un quadrato a partire da p2+q2 quadrati uguali di lato a.
Si taglia il quadrato grande in tre parti: un rettangolo AEFD di lati a e b (che poi si taglia in due con una diagonale), un rettangolo EBHG di lati b e a−b, e un quadrato CFGH di lato a−b. Si porta poi il rettangolo EBHG in JMNK accanto al quadrato IJKL, ottenendo un altro rettangolo IMNL che si divide in due con una diagonale, disponendo poi le parti opportunamente (fig. 18).
Le figure che abbiamo ricordato permettono per sovrapposizione, simmetria e ripetizione di ottenere tassellature del piano. Un trattato persiano anonimo intitolato Fī tadāḫul al-aškāl al-mutašābiha wa-'l-mutawāfiqa (Sugli ornamenti a intreccio di figure simili e congruenti), verosimilmente dei primi del XIV sec., che segue, nella collezione persiana 169 della Bibliothèque Nationale di Parigi, una versione persiana dell'XI sec. del trattato di Abū 'l-Wafā᾽ al-Būzǧānī, riprende una parte di queste figure per ottenere arabeschi e ornamenti a intreccio. Tali figure si ritrovano anche nel rotolo di Topkapı che risale probabilmente al periodo timuride (fine XV-inizio XVI sec.). Questo rotolo, che presenta in un'impostazione standardizzata, ripetibile e flessibile, motivi fatti di intrecci di stelle e di poligoni, è verosimilmente un repertorio di disegni geometrici per superfici e volte piuttosto che di disegni preparati per edifici specifici.
Tassellature dello stesso tipo si trovano anche nell'Andalus nel corso del XIV e del XV sec., in particolare nelle decorazioni murali, nelle muqarnas dell'Alhambra di Granada o della moschea di Cordoba. Uno stile di decorazioni che continua in Marocco dopo la caduta del regno dei Nasridi. Lo studio matematico delle simmetrie e delle periodicità di queste tassellature regolari di mosaici, nelle quali intervengono i colori, ha permesso ai matematici contemporanei di determinare diciassette strutture di base per la creazione di certi disegni simmetrici e ha dato origine al concetto di gruppo cromatico o gruppo caleidoscopico.
Misure di lunghezza, superficie e volume nei trattati di 'ḥisāb'
Se il trattato di al-Būzǧānī è praticamente la sola opera dedicata alle costruzioni geometriche che ci sia pervenuta, le cose stanno diversamente per quanto riguarda le opere di ḥisāb (scienza del calcolo), l'elenco delle quali sarebbe lunghissimo. Tutte queste opere contengono un capitolo riguardante la misura di lunghezze, superfici e volumi. Tra queste ricordiamo in particolare quelle di al-Karaǧī, dal titolo al-Kāfī fī 'l-ḥisāb (Il sufficiente per il calcolo), di al-Fārisī Asās al-qawā῾id fī uṣūl al-fawā᾽id (I fondamenti delle regole nei principî delle utilità) e di al-Kāšī, il cui trattato Miftāḥ al-ḥisāb (La chiave del calcolo) è in un certo senso il punto d'arrivo di questa tradizione che ha origine nella seconda parte del Kitāb al-ǧabr wa-'l-muqābala (Libro dell'algebra) di al-Ḫwārizmī.
Quest'ultimo trattato contiene nella seconda parte (ossia quella non tradotta in latino), oltre a problemi di eredità e di transazioni commerciali, un capitolo intitolato Fī 'l-misāḥa (Sulla misurazione) nel quale al-Ḫwārizmī riporta sinteticamente, senza darne la dimostrazione, alcune misure di superficie (quadrato, rettangolo, triangolo, cerchio, settore circolare e segmento di cerchio) e di volume (cubo, cilindro, cono, piramide).
Al-Karaǧī (oppure al-Karḫī), che fu attivo tra X e XI sec., è autore di numerose opere di algebra nelle quali viene sviluppata la teoria del calcolo algebrico.
Nel trattato intitolato al-Kāfī fī 'l-ḥisāb, dopo alcuni capitoli sull'aritmetica e prima dell'ultima parte dedicata alla risoluzione delle equazioni quadratiche e al calcolo algebrico, vi sono nove capitoli sul calcolo di aree e volumi, e un capitolo su come misurare piccoli dislivelli. Vi sono le definizioni dei termini geometrici elementari (diagonale, triangolo, ecc.), ma le formule di calcolo sono quasi sempre date senza dimostrazione. A volte una figura serve a giustificare il risultato.
Kamāl al-Dīn al-Fārisī, allievo dell'astronomo e matematico Quṭb al-Dīn al-Šīrāzī, è noto soprattutto per lavori di ottica. È anche autore di lavori di teoria dei numeri e di algebra. Il suo trattato dal titolo Asās al-qawā ῾id si inserisce nel solco dell'opera precedente, sia per commentarla sia per criticarla, riprendendone anche alcune formule. Si ricordano le definizioni della maggior parte delle figure geometriche e dei termini adottati, spesso negli stessi termini delle definizioni euclidee, e anche alcune dimostrazioni, mentre per altre si rimanda agli Elementi di Euclide, alle opere di Archimede e alle Sferiche di Teodosio.
Al-Kāšī, originario di Kashan, è stato direttore dell'Osservatorio di Samarcanda all'epoca di Uluġ Beg; è una delle ultime grandi figure della scienza araba. La sua opera Miftāḥ al-ḥisāb è una sorta di compendio di tecniche di calcolo che si propone di essere completo. Il Libro IV, intitolato Fī 'l-misāḥa, presenta, senza dimostrazione, algoritmi di calcolo (esatto e approssimato) di aree e di volumi di superfici e di solidi dei più diversi, e vi si ritrova la padronanza delle tecniche di calcolo più sofisticate di cui al-Kāšī dà prova in altre sue opere: nella Risāla al-muḥīṭiyya (Epistola sulla circonferenza), nella quale determina π con 16 decimali esatti (mediante poligoni inscritti e circoscritti di 3×228 lati), nel FĪ 'l-watar wa-'l-ǧayb (Sulla corda e il seno) nel quale calcola il seno di 1° con la stessa precisione, o negli Zīǧ-i Ḫāqānī (Tavole astronomiche per Ḫāqān), che presentano una tavola dei seni a quattro cifre sessagesimali esatte. Questa grande precisione nei calcoli numerici, caratteristica della scuola di Uluġ Beg a Samarcanda, segna l'apogeo della padronanza del calcolo nei paesi dell'Islam.
I tre trattati di ḥisāb hanno in comune il fatto di rivolgersi a utenti capaci di applicare tali tecniche di calcolo. Tra questi vi sono presumibilmente un gran numero di segretari amministrativi (kuttāb), una classe istruita e colta al punto che un autore può rinviare, per alcune dimostrazioni, agli Elementi di Euclide o alle opere di Archimede. Se i principî della misura sono ricordati rapidamente, l'unità di lunghezza è sempre precisata, e in genere è il cubito: l'unità di misura di superficie è allora il quadrato del cubito e quella di volume il cubo di un cubito di lato. Alcuni autori (per es., al-Fārisī) parlano di altre unità di misura (cubiti vari, canna, palmo, dito), e danno esempi di conversione da un'unità all'altra. Le formule ‒ senza dimostrazione (come in al-Kāšī), con un'indicazione sommaria di dimostrazione (al-Karaǧī), o con dimostrazioni più particolareggiate (al-Fārisī) ‒ sono sempre illustrate con esempi numerici.
La misura delle lunghezze
Salvo il caso della misura della circonferenza, per la quale tutti questi autori prendono 3+1/7 come valore approssimato di π, e la misura degli archi, sulla quale torneremo, la misura delle linee (rette), contrariamente a quella delle superfici e dei volumi, non risulta da un calcolo ma da una misura diretta. Al-Kāšī precisa che il valore 3+1/7 è scelto per comodità e dà 3+8/60+29/602+44/603 come valore di π, valore che usa nella maggior parte dei calcoli. Al-Fārisī, seguito da al-Kāšī, suggerisce che si può avere un'idea del rapporto della circonferenza al diametro mediante il 'procedimento ingegnoso' che consiste nel misurare la circonferenza con un filo la cui lunghezza viene confrontata con il diametro.
La misura delle superfici
Dopo aver ricordato le formule che danno le misure dei quadrati e dei rettangoli, che sono alla base di tutti i calcoli delle aree, una parte notevole di questi trattati è dedicata all'area dei triangoli. Ciò è giustificato dal fatto che la superficie di un qualunque poligono si ottiene decomponendolo in triangoli.
La prima formula che dà l'area di un triangolo (altezza per la metà della base corrispondente), presente in tutti questi trattati fin da al-Ḫwārizmī, pone due problemi pratici: sapere se il piede dell'altezza cade o no all'interno della base corrispondente (da cui la necessità sia di determinare la natura del triangolo, sia di prendere sempre come base il lato più lungo), e determinare l'altezza.
La natura del triangolo si determina con una generalizzazione del teorema di Pitagora: se BC è il lato più lungo del triangolo ABC, il triangolo è rettangolo, acutangolo od ottusangolo a seconda che AB2+AC2 sia uguale, maggiore o minore di BC2. Questo metodo generalizza quello applicato in un caso particolare dagli artigiani per verificare la perpendicolarità di una squadra, e si trova in tutti questi trattati di ḥisāb.
Per determinare l'altezza al-Ḫwārizmī aveva esposto su un esempio numerico paradigmatico (AB=13, BC=14 e AC=15 cubiti), che talvolta i suoi successori (per es., al-Karaǧī) riprenderanno, un metodo algebrico di calcolo di AH, altezza relativa al lato BC, ponendo BH=x (la 'cosa') e utilizzando le regole di calcolo sui polinomi di grado inferiore o uguale a 2 descritte nella prima parte del trattato. I suoi successori preferiranno per la maggior parte dare un calcolo di BH dedotto da Elementi, II, 12 (triangoli ottusangoli, AC2= AB2+BC2+2BC××BH) e II, 13 (triangoli acutangoli AC2=AB2+BC2−2BC××BH), o come al-Kāšī, utilizzare il seno [AH=(senB/60)AB]. Al-Kāšī è d'altronde il solo dei nostri autori a utilizzare sistematicamente nei calcoli il seno (nella Miftāḥ egli presenta una tavola dei seni).
La formula di Erone "se p è il perimetro di un triangolo di lati a, b e c, l'area s del triangolo è data dalla formula":
,
sull'origine della quale anche un traduttore che conosceva perfettamente il greco come Ṯābit ibn Qurra (IX sec.) è incerto (tra India o Bisanzio), e che matematici più tardi come al-Bīrūnī attribuiscono ad Archimede, viene dimostrata nel IX sec. nel trattato dei Banū Mūsā Kitāb Ma῾rifat misāḥat al-aškāl al-basīṭa wa-'l-kuriyya. Assente dal trattato di al-Ḫwārizmī, si trova, senza dimostrazione, negli altri trattati di ḥisāb che ricordiamo in questa sede.
Gli autori si soffermano poi, chi più chi meno, su calcoli di aree di triangoli particolari (rettangoli, isosceli, equilateri), adducendo il fatto che vi possono essere metodi più adatti a questi casi particolari e che quindi è opportuno applicare. Al-Fārisī, come al-Kāšī, tratta dettagliatamente il triangolo equilatero (calcolo dell'area dati il lato o l'altezza, del lato data l'area, ecc.), precisando inoltre che, se il lato del triangolo equilatero ha per misura un numero razionale, l'altezza e l'area sono numeri irrazionali. Ciò offre inoltre a questi due autori l'occasione di mostrare la loro abilità nel calcolo numerico, fornendo l'uno un valore di √3/4, esatto a meno di 60−4 e, l'altro, uno esatto a meno di 60−5.
a) I quadrilateri. Anche se l'area di un quadrilatero qualunque si può calcolare decomponendolo in triangoli, tutti questi autori danno ugualmente le formule ben note delle aree di vari quadrilateri (quadrato, rettangolo, rombo, parallelogramma, trapezio). Alcuni, tra cui al-Karaǧī e soprattutto al-Fārisī, ricordano inoltre le proprietà caratteristiche delle diagonali. Riguardo al trapezio, al-Fārisī dimostra nei tre casi (trapezio rettangolo, isoscele o qualunque) la formula che dà il calcolo dell'altezza in funzione dei lati.
b) I poligoni. Riguardo ai poligoni nei quali si può inscrivere un cerchio, la formula s=(1/2)d(1/2)p (dove p è il perimetro del poligono, d il diametro del cerchio inscritto) viene data da tre autori (al-Fārisī dimostra inoltre che ogni poligono regolare si può inscrivere in un cerchio). Questa formula, dimostrata dai Banū Mūsā nel corso della dimostrazione dell'area del cerchio, richiede che si determini il diametro del cerchio inscritto nel poligono.
Anche al-Kāšī, utilizza questo metodo nel caso particolare di un triangolo: il raggio del cerchio inscritto in un triangolo ABC è allora
e indica, per un poligono qualunque nel quale si può inscrivere un cerchio, il valore del raggio r di questo cerchio: sia AB un lato, A e B gli angoli di vertici A e B, allora
Si trova in al-Karaǧī una buona formula che dà il diametro del cerchio circoscritto a un poligono regolare. Se c è il lato del poligono, n il numero dei lati, D il diametro del cerchio circoscritto, allora
,
da cui si deduce facilmente il diametro del cerchio inscritto. Questa formula ha il difetto di essere esatta solo per n=3,4, o 6 come fa notare al-Fārisī, il quale mostra come sia falsa per l'ottagono, rimandando per il caso generale alla tavola degli archi e delle corde date in precedenza. Osserviamo tuttavia che per n=5, 7 o 8 la formula di al-Karaǧī dà il risultato con un'approssimazione abbastanza buona (ciò equivale a porre
,
che per grandi valori di n significa prendere π ≅ 3).
Al-Kāšī presenta una tavola che dà il rapporto al lato, rispettivamente, del diametro del cerchio inscritto e della superficie del poligono, per n=5,6,7,8,9,10,12,15,16 e 25.
c) Area del cerchio, dei settori circolari, dei segmenti di cerchio. La formula che dà l'area del cerchio,
(dove d il diametro del cerchio e p la circonferenza), si trova senza dimostrazione in tutti gli autori considerati. Se alcuni, come per esempio al-Fārisī, l'attribuiscono ad Archimede, al-Ḫwārizmī invece la giustifica per analogia con i poligoni regolari circoscritti a un cerchio. Si trovano anche le formule approssimate
(al-Ḫwārizmī, al-Karaǧī, al-Fārisī), ovvero
(al-Karaǧī), entrambe corrispondenti al valore approssimato 3+1/7 di π. Al-Kāšī dà, con il suo valore approssimato di π, una tavola dei valori del perimetro e dell'area in funzione del diametro.
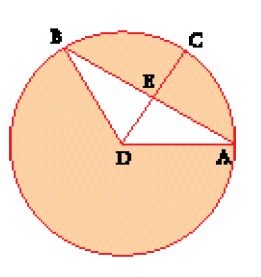
Il calcolo dell'area del settore circolare ((1/2)d∙(1/2)a, dove a è la lunghezza dell'arco e d il diametro del cerchio) o del segmento circolare (area del settore più o meno l'area del triangolo corrispondente a seconda che l'arco sia minore o maggiore di una semicirconferenza, fig. 19) richiede innanzi tutto di sapere se un arco di circonferenza è uguale, minore o maggiore di una semicirconferenza (a seconda che la freccia dell'arco sia uguale, minore o maggiore del raggio), e pone il problema del calcolo del diametro del cerchio note la corda e la freccia dell'arco, come pure quello del calcolo della lunghezza dell'arco.
La determinazione del diametro del cerchio, note la corda e la freccia (fig. 20), si trova da al-Ḫwārizmī in poi in tutti i trattati:
Viene dimostrata da al-Fārisī, che a questo scopo utilizza esplicitamente la prop. 35 del Libro III degli Elementi.
Per quanto riguarda la determinazione dell'arco (problema non affrontato da al-Ḫwārizmī), al-Karaǧī comincia con il ricordare come si determinano alcune corde (π/3, 2π/3, π/2, π/6, 5π/6, ecc.), determinazioni che si basano sul teorema di Tolomeo, che egli richiama (la somma dei prodotti dei lati opposti di un quadrilatero inscritto in un cerchio è uguale al prodotto delle diagonali). Per piccoli valori dell'arco a⌢ dà poi una formula di approssimazione che equivale a porre
Per la determinazione dell'arco al-Fārisī e al-Kāšī rimandano alla consultazione della tavola delle corde (al-Fārisī) o dei seni (al-Kāšī), che figurano nelle rispettive opere. Presentano anche il metodo per calcolare la superficie di una lente e della mezzaluna, al quale al-Kāšī aggiunge anelli e varie figure piane composte di poligoni e archi di cerchio: scale, stelle, fiori, tamburi, e così via.
d) Superfici non piane. Riguardo alle superfici non piane (sfera, calotta sferica, cilindro retto od obliquo, cono retto, tronco di cono retto a basi perpendicolari all'asse) che non figuravano in al-Ḫwārizmī, tutti questi autori ricordano le formule dimostrate da Archimede, dai Banū Mūsā o da Ṯābit ibn Qurra. Al-Kāšī aggiunge a queste formule una formula di calcolo approssimato della superficie di un cono obliquo della quale afferma di essere l'autore.
Misura dei volumi
Le formule da cui si ottengono il volume del cubo e del parallelepipedo rettangolo sono alla base dei calcoli di volume. Tutti questi studiosi ricordano le formule ben note, alcune fin dagli Elementi, che danno il volume di un prisma e di un parallelepipedo, di un cilindro retto od obliquo, di una piramide e di un tronco di piramide retta od obliqua, di un cono o di un tronco di cono retto od obliquo, di una sfera e di una calotta sferica. Il calcolo di alcuni di questi volumi richiede di determinare preventivamente l'altezza; soltanto al-Kāšī indica come calcolarla mediante il seno dell'angolo formato dall'asse, o da una generatrice, con il piano di base. Dopo di che, così come aveva fatto per le superfici dei poligoni regolari, al-Kāšī dà, sotto forma di tavola, l'algoritmo di calcolo ‒ a partire dal diametro ‒ dei volumi dei vari poliedri regolari e semiregolari inscritti in una sfera.
Al-Fārisī e al-Kāšī segnalano inoltre che è possibile conoscere il volume di un corpo conoscendone il peso e il peso specifico (peso di un cubo di 1 cubito di lato). A questo scopo danno una tavola dei pesi specifici di una trentina di sostanze (per es., oro, mercurio, piombo, argento, rame, ottone, ferro, vetro, ma anche miele, latte vaccino, acqua, olio, e così via).
Superfici e volumi di elementi architettonici
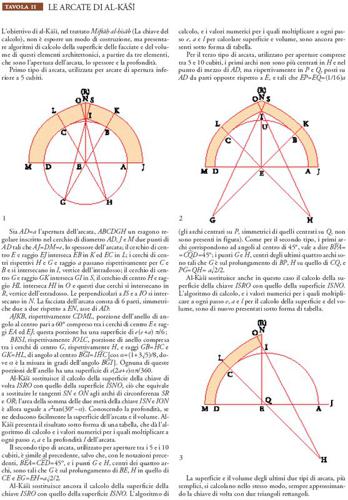
a) Arcate e portici a volta. È nota l'importanza di questi elementi nell'architettura dei paesi dell'Islam e in particolare nell'architettura timuride (īwān). Le arcate si distinguono dai passaggi a volta soltanto per il rapporto tra apertura e profondità: se la profondità è inferiore all'apertura siamo in presenza di un'arcata, altrimenti di un portico a volta.
L'argomento è affrontato molto brevemente da al-Karaǧī e al-Fārisī, che calcolano la superficie della facciata e il volume di un portico a volta in cui l'intradosso e l'estradosso sono estradossati (gli archi interni ed esterni che si corrispondono sono concentrici), ognuno costituito da due archi spezzati (volta ogivale). Il calcolo della superficie della facciata (semisomma dell'arco interno ed esterno moltiplicata per lo spessore dell'arco), dal quale si deduce facilmente il volume, dà un eccellente valore approssimato, ma lascia intatto il problema della misura di questi archi.
Al-Kāšī da parte sua definisce cinque tipi di archi e di portici a volta con intradosso ed estradosso estradossati. Per due di questi intradosso ed estradosso sono composti ciascuno da due archi spezzati (il primo un'ogiva in terzo punto e il secondo un'ogiva ribassata), per gli altri tre l'estradosso e l'intradosso sono composti ciascuno da quattro archi. Questi ultimi tre tipi sono utilizzati, rispettivamente, per aperture inferiori a 5 cubiti, comprese tra 5 e 10 cubiti, superiori a 10 cubiti (Tav. II).
b) Cupole. Al-Kāšī distingue quattro tipi di cupole, calcolando per ognuno di questi la superficie degli estradossi e degli intradossi e il volume della parte edificata. I quattro tipi di cupole sono i seguenti: cupole costituite da una semisfera cava, cupole costituite da un segmento di sfera cava, cupole piramidali e cupole ottenute facendo ruotare attorno all'asse di simmetria le arcate che abbiamo ora descritto.
Le superfici e i volumi dei primi tre tipi di cupole sono stati calcolati in precedenza. Per quanto riguarda il quarto tipo, al-Kāšī propone un metodo di calcolo approssimato, tanto della superficie (interna ed esterna) quanto del volume. Questo metodo equivale al calcolo di una somma di Riemann.
Si tracciano sulla superficie (interna o esterna) della cupola dei cerchi aventi come polo il vertice di questa superficie (uno di questi cerchi deve passare per il punto B delle figg. II. 1, 2, punto di raccordo degli archi quando l'arcata è composta di quattro archi); sia per la superficie che per il volume ogni porzione di cupola compresa tra due cerchi consecutivi viene assimilata a una sezione di cono a base circolare. Al-Kāšī afferma che per ottenere un buon valore approssimato è sufficiente tracciare 7 od 8 cerchi sull'estradosso e sull'intradosso.
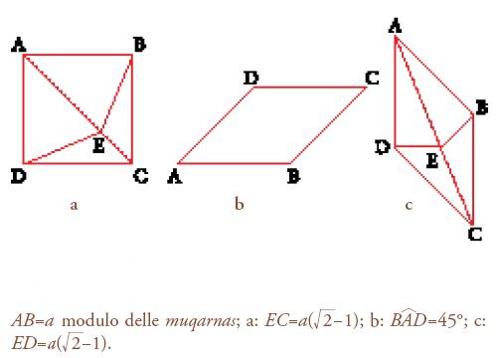
c) Muqarnas. Le muqarnas, figure geometriche studiate recentemente da Y. Dold-Samplonius (1992), sono elementi decorativi tipici dell'architettura islamica orientale (i loro equivalenti nell'architettura del Maghreb si chiamano muqarba). Constano di serie di celle alveolari disposte in strati sovrapposti a formare una sorta di raccordo tra la base circolare delle cupole e la struttura di base, quadrata o poligonale, dei muri inferiori dell'edificio. Se ne incontrano anche nell'architettura timuride come elemento decorativo in cima ai minareti (per es., quello della Madrasa di Uluġ Beg). Di origine probabilmente abbaside, questo tipo di elemento architettonico si diffonderà nel mondo iranico e in Asia centrale. Le muqarnas sono costituite da celle di base disposte su vari livelli e composte da elementi piani o ricurvi, che formano piani laterali, e da un tetto. Al-Kāšī distingue quattro tipi di muqarnas, due a faccette piane e due a faccette curve.
Muqarnas a faccette piane, dette di tipo minbar o 'rivestite d'argilla' (come le muqarnas di certi antichi edifici di Isfahan): le seconde differiscono dalle prime solo per il fatto che i livelli non hanno tutti la stessa altezza. Le faccette sono figure piane, come quelle descritte in precedenza e delle quali si è calcolata la superficie (rombi, parallelogrammi, rettangoli per i piani laterali delle cellule, quadrati, rombi, mandorle, semiquadrati, semirombi, bipodi per i tetti). Il calcolo della superficie di queste cellule si riporta perciò a quelli precedenti, e sarà fatto dunque in funzione del lato di un elemento di base di ciascun piano, detto modulo della muqarnas.
Muqarnas a faccette curve: muqarnas dette curve (solo le faccette dei tetti e gli elementi tra due cellule ‒ triangoli ‒ sono incurvati, mentre i piani laterali delle cellule sono costituiti esclusivamente da quadrati e da rettangoli), e muqarnas dette di tipo šīrāzī, più complesse e a elementi più variati.
Per calcolare le superfici degli elementi incurvati al-Kāšī è portato a definire un coefficiente di curvatura. A questo scopo ricorda il 'metodo del muratore' per tracciare le muqarnas curve, un metodo utilizzato anche nell'architettura timuride per costruire un certo numero di arcate.
Sia ABCD un rettangolo tale che BC=2AB=2a, AE tale che BAE=30°, G un punto di AE tale che AG=(3/5)AE, EH=EG, I il centro del cerchio tangente ad AE in G e a BC in H: la linea AGH definisce il coefficiente di curvatura della muqarnas.
Sia AB=a, il modulo della muqarnas,
,
,
e infine
il coefficiente di curvatura della muqarnas. Il calcolo di al-Kāšī equivale allora ad assimilare la superficie curva generata dalla linea AGH a un triangolo di base a e altezza (1/2)AGH.
La misura di piccoli dislivelli
Al-Karaǧī e successivamente al-Fārisī descrivono, praticamente negli stessi termini, un metodo che consente di calcolare dei piccoli dislivelli, per esempio per scavare un canale di pendenza abbastanza lieve.
Si costruisce uno strumento che permette di misurare l'orizzontalità: una tavola di legno lunga 1 cubito, larga 2 dita, e dello spessore di 1 dito è bucata per tutta la lunghezza (per potervi infilare una corda). A questa tavola è fissato un triangolo isoscele di metallo, con il vertice diretto verso il basso, al centro della cui base, disposta sul lato lungo della tavola, è fissato un filo a piombo (la tavola è quindi orizzontale quando il filo a piombo passa per il vertice del triangolo). Si infila in questo strumento una corda di 15 cubiti, alle due estremità della quale sono fissate due tavolette graduate di uguale lunghezza. Due uomini che tengono ciascuno una tavoletta si allontanano di una distanza pari alla lunghezza della corda da tendere (le tavolette sono tenute verticali e appoggiate a terra). Se il filo a piombo si sovrappone al vertice del triangolo, le due tavolette sono alla stessa altezza, altrimenti l'uomo che si trova dal lato del vertice del triangolo isoscele (cioè dal lato più alto) abbassa la corda lungo la tavoletta fino a ottenere l'orizzontalità (avvicinandosi leggermente all'altro uomo). L'altezza letta sulla graduazione dà allora la differenza di dislivello tra i due luoghi. Si possono in questo modo misurare gradatamente dei piccoli dislivelli.
Il trattato di Ibn al-Hayṯam 'Fī uṣūl al-misāḥa' e i procedimenti stereometrici
I principî della misura
Nel trattato Fī uṣūl al-misāḥa (Sui principî della misura), che Roshdi Rashed non esita a definire un evento storico ed epistemologico, Ibn al-Hayṯam (m. dopo il 1040) si propone di fondare l'arte della misura su solide basi. Egli definisce la misura insistendo sul fatto che l'unità scelta è arbitraria e stabilisce una netta distinzione tra grandezze (soltanto linee, superfici e solidi) e misura di queste grandezze (numeri interi o frazionari), mentre per esempio nei trattati di ḥisāb le grandezze sono trattate implicitamente come numeri alla maniera degli algebristi. Non affronta, a proposito della misura delle rette, il problema dell'incommensurabilità delle linee (forse perché il problema non si pone per il misuratore che, se ha sulla riga una graduazione sufficientemente fine, può attribuire una misura a qualunque segmento di retta); lo affronterà in seguito, quando si proporrà di calcolare il rapporto tra un arco di circonferenza e un quarto della stessa:
Quanto all'arco di cerchio la quantità della sua misura è nota quando è noto il rapporto con l'intera circonferenza […]. Tuttavia per un arco qualunque il rapporto con il cerchio può non essere un rapporto numerico […] se l'arco è di questo tipo non lo si può quindi esprimere; se ciò accade nella misura allora il rapporto tra l'inesprimibile (nisba ġayr al-manṭiq) conduce a ciò che si esprime con un rapporto tale che non vi sia tra questo e il rapporto vero uno scarto che comporti conseguenze. Analogamente, se una grandezza è inesprimibile (ġayr manṭiq), allora essa conduce a quanto si esprime con una grandezza tale che non ci sia tra quella e questa uno scarto che comporti conseguenze. E ciò perché l'arte pratica non si può realizzare senza che vi sia una qualche approssimazione quando non è possibile un'estrema esattezza […]. Questa via […] è quella di stringere l'apertura del compasso il più possibile. Allora se si diminuisce l'apertura del compasso si giunge necessariamente a una grandezza che misura i due archi anche se il rapporto non è un rapporto numerico. Infatti se le parti diventano sempre più piccole, la differenza per cui uno dei due archi supera l'arco che ha un rapporto con l'altro arco diventa sempre più piccola fino a diventare insensibile. (Rashed 2000a, pp. 584-590)
L'arte del geometra
Ibn al-Hayṯam definisce il campo di applicazione del geometra: sono di sua competenza la misura delle superfici piane (esclusivamente poligoni, cerchi, settori e segmenti circolari), dei poliedri, dei cilindri a base circolare, dei coni a base circolare e delle sfere. Contrariamente a quanto sono soliti fare gli autori dei trattati di ḥisāb, Ibn al-Hayṯam non moltiplica i casi particolari ma, al contrario, cerca di enunciare e dimostrare un numero minimo di risultati generali ai quali ridurre tutti i casi particolari: i poligoni si decompongono in triangoli e i poliedri in piramidi. L'impostazione è in qualche modo inversa di quella di al-Kāšī: non si tratta di dare un repertorio il più completo possibile di formule il più possibile precise di una gran quantità di superfici e di solidi, ma di offrire al geometra i mezzi perché possa ritrovare da solo i risultati dei quali ha bisogno. Sarà dunque essenziale per lui la misura dei triangoli e delle piramidi.
Riguardo alle superfici Ibn al-Hayṯam dimostra tutte le formule che presenta, compresa la formula di Erone e quella per l'area del cerchio. Se non entra nei particolari del calcolo delle aree dei vari poligoni (rombi, parallelogrammi, trapezi, poligoni regolari, ecc.), insiste invece sui vincoli materiali che incontrano le misurazioni (ostacoli, grandi distanze, facce nascoste, ecc.) e che possono impedire di misurare il terzo lato di un triangolo o la corda di un poligono, e fornisce un procedimento per determinare queste grandezze senza misurarle direttamente (nella tradizione di ciò che fa Euclide nella prop. 21 dell'Ottica).
Supposte note le lunghezze BA e BC, si vuole conoscere la lunghezza AC senza misurarla direttamente. Sia D un punto di BC tale che la misura di BD sia di 1 cubito. Si prenda su BA un punto E tale che
e si misuri DE; allora AC̅=DE̅∙BC̅.
Ibn al-Hayṯam risolve in modo analogo, riguardo al volume dei poliedri, il problema della determinazione delle corde di un poligono, allo scopo di decomporre la base di questi solidi in triangoli anche quando questa base non è accessibile (faccia inferiore). Si prende un punto E sul prolungamento di AB in modo che la misura di AE sia di un cubito, e un punto D sul prolungamento di AC in modo che
e si misura DE; allora BC̅=DE̅̅∙AB̅.
Riguardo ai volumi, il parallelepipedo rettangolo è la base per il calcolo delle superfici. Contrariamente a quanto fatto per le superfici, sui volumi Ibn al-Hayṯam non dimostra in questo trattato alcun risultato, rimandando il lettore agli Elementi di Euclide o alle opere di Archimede. I poliedri si decompongono in piramidi. Il solo problema che pone allora il calcolo dei volumi è la determinazione dell'altezza della piramide, del cono o del cilindro. Per il calcolo di queste altezze egli espone, oltre a uno geometrico, un procedimento stereometrico.
La determinazione stereometrica delle altezze
Il punto di partenza dei trattati arabi sulle misurazioni ottiche è l'Ottica di Euclide (tradotta in arabo fin dal IX sec., come la Catottrica di Erone di Alessandria). Quest'opera contiene quattro proposizioni di carattere stereometrico, le proposizioni dalla 18 alla 21:
Prop. 18: essendo visibile il Sole, determinare la misura di un'altezza data (ombra).
Prop. 19: determinare la misura di una data altezza quando il Sole è nascosto (specchio).
Prop. 20: determinare la misura di una data profondità.
Prop. 21: determinare la misura di una data lunghezza.
Tali proposizioni furono riprese da al-Kindī nell'opera Fī taqwīm al-ḫaṭa' wa-'l-muškilāt allatī li-Uqlīdis fī 'l-Manāẓir. Questi studi stereometrici saranno proseguiti da Sinān ibn al-Fatḥ nel IX sec. (con l'opera Fī 'l-misāḥāt al-manāẓiriyya, Sulle misurazioni ottiche), poi da al-Qabīṣī nel X sec. e infine da Ibn al-Hayṯam il quale, oltre che nel trattato Fī uṣūl al-misāḥa, vi ritorna in due altri trattati: Fī ma῾rifat irtifā῾ al-ašḫāṣ al-qā᾽ima wa-a῾mida al-ǧibāl wa-irtifā῾ al-ġuyūm (Sulla conoscenza degli oggetti elevati, dell'altezza delle montagne e delle nuvole) e Fī istiḫrāǧ a῾mida al-ǧibāl (Sulla determinazione dell'altezza delle montagne). Più che di oggetti geometrici (piramidi, cilindri, coni, ecc.), si tratta di misurare le altezze di oggetti materiali (muri, edifici, montagne e così via).
Sinān ibn al-Fatḥ nel trattato Fī 'l-misāḥāt al-manāẓiriyya determina, con metodi molto vicini a quelli che si trovano nell'Ottica di Euclide (triangoli simili), la lunghezza di una retta orizzontale, di una verticale e la profondità di una fossa.
Al-Qabīṣī, invece, in un passo intitolato anch'esso Fī 'l-misāḥāt al-manāẓiriyya, mostra in che modo sia possibile determinare l'altezza di una montagna la cui base è irraggiungibile, servendosi di un astrolabio (che permette di misurare angoli e seni).
Il metodo è il seguente. Sia AI=BK=60 (equivalente all'unità di calcolo), IJ=Senα, AJ=Sen(90°−α), KL=Senβ, BL=Sen(90°−β), con valori dati dall'astrolabio. Si misuri AB; allora
,
ovvero
,
infatti
,
da cui il risultato.
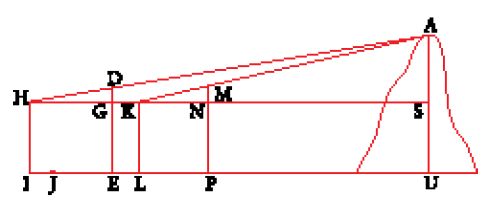
La tecnica esposta da Ibn al-Hayṯam riprende questo principio della doppia misura senza utilizzare l'astrolabio, ma mediante un'asta graduata infilata in terra e un filo a piombo per determinare la verticale.
Sia HI=KL=GE=NP (fig. 29) la distanza tra l'occhio dell'osservatore e il suolo, misurata con un filo a piombo e riportata sull'asta, DE=MP, inserita nel terreno in modo che DG̅=MN̅=1 cubito. L'osservatore pianta l'asta nel suolo nel punto P, quindi indietreggia finché l'occhio, ovvero il punto K, il punto M cima dell'asta, e il punto A non sono allineati. Segna allora la propria posizione in L, pianta l'asta in terra nel punto E e ripete l'operazione segnando la propria posizione in I. Ne segue che:
,
da cui
posto EJ=PL,
da cui deriva
,
e dunque IL∙EI=HS∙IJ; HS∙GD=AS∙HG; ma GD̅=1, e quindi HS̅=AS̅∙HG̅ e IL̅∙EI̅̅=AS̅∙HG̅∙IJ̅. Ma HG=IE, e dunque IL̅=AS̅∙IJ̅, pertanto:
Ibn al-Hayṯam riprende questo metodo in altri due trattati, Fī ma῾rifat irtifā῾ al-ašḫāṣ al-qā᾽ima wa-a῾mida al-ǧibāl wa- irtifā῾ al-ġuyūm e Fī istiḫrāǧ a῾mida al-ǧibāl: il primo è essenzialmente geometrico, il secondo invece è molto tecnico e privo di dimostrazioni, e si rivolge direttamente agli artigiani precisando gli aspetti pratici fin nei più piccoli dettagli (lunghezza dell'asta, modo di fare i segni in terra, ecc.).
Conclusioni
I trattati di geometria pratica dei quali abbiamo parlato sono molto diversi tra loro, tanto per gli obiettivi quanto per il pubblico al quale si rivolgono. Si dividono in varie categorie: manuali, scritti da eminenti matematici e che hanno lo scopo di spiegare agli artigiani, senza dimostrazioni, procedimenti pratici (è il caso di Ibn Sinān o di al-Būzǧānī) o, al contrario, opere che, sempre rivolgendosi a dei tecnici (geometri), si propongono di dare un fondamento teorico a pratiche già in uso (è il caso del trattato di Ibn al-Hayṯam) o, ancora, raccolte di procedimenti di calcolo (come i trattati di ḥisāb). Essi ci permettono di avere un'idea di quali potevano essere il bagaglio scientifico e le attrezzature di cui disponevano le diverse categorie sociali a cui si rivolgevano, e riguardo alle quali le testimonianze che abbiamo sono molto scarse. Si tratta di artigiani che lavorano a mano, come dice Ibn Sinān, cioè che fanno costruzioni geometriche, anche complesse, a partire da conoscenze teoriche modeste; di personale amministrativo più colto che vuole precisione nei calcoli; di geometri capaci di seguire dimostrazioni difficili pur affrontando problemi pratici. Quanto agli strumenti, il kātib dispone di tavole di seni e di pesi specifici, ecc., delle quali il trattato di al-Kāšī fornisce gli esempi più numerosi: per l'artigiano la riga, il compasso e la squadra; per il geometra la riga graduata e la cordicella per la misura delle distanze, il filo a piombo per determinare la verticale o lo strumento descritto da al-Fārisī per misurare i dislivelli. Il geometra verifica la perpendicolarità applicando il teorema di Pitagora senza ricorrere alla squadra (non deve tracciare angoli retti, a parte le verticali che però ottiene con il filo a piombo), teorema che serve anche agli artigiani per verificare la precisione di una squadra.
Il compasso si poteva usare anche per la misura degli archi: sembra anzi che questa sia stata la pratica corrente degli artigiani e dei geometri (Abū 'l-Wafā᾽ al-Būzǧānī rimprovera gli artigiani per questo fatto). L'uso del solo astrolabio per la misura degli angoli è menzionato da al-Qabīṣī nel trattato Fī 'l-misāḥāt al-manāẓiriyya.
Bibliografia
Aghayani-Chavoshi 1996: Aghayani-Chavoshi, Jafar, L'oeuvre scientifique d'Abû Wafâ al-Buzjânî (Thèse de doctorat, Paris VII, 1996).
Dold-Samplonius 1992: Dold-Samplonius, Yvonne, Practical Arabic mathematics. Measuring the Muqarnas by al-Kāshī, "Centaurus", 35, 1992, pp. 193-242.
Garrido 1987: Garrido, C. Ruiz - Gomez, Rafael P., Visiones matematicas de la Alhambra. El color, "Epsilon", 9, 1987, pp. 51-59.
Heath 1921: Heath, Thomas L., A history of Greek mathematics, Oxford, Clarendon, 1921, 2 v. (rist.: New York, Dover, 1981, 2 v.).
Knorr 1989: Knorr, Wilbur R., Textual studies in ancient and medieval geometry, Boston-Basel-Berlin, Birkhäuser, 1989.
Necipoglu 1995: Necipoglu, Gülru, The Topkapi scroll, Geometry and ornament in islamic architecture. Topkapi palace museum library ms. H 1956, Santa Monica (Cal.), Getty Center for the history of art and the humanities, 1995.
Neugebauer 1999: Neugebauer, Otto - Rashed, Roshdi, Sur une construction du miroir parabolique par Abū al-Wafā᾽ al-Būzjānī, "Arabic sciences and philosophy", 9, 1999, pp. 261-277.
Özdural 2000: Özdural, Alpay, Mathematics and arts: connections between theory and practice in the medieval islamic world, "Historia mathematica", 27, 2000, pp. 171-201.
Rashed 1993: Rashed, Roshdi, Géométrie et dioptrique au Xe siècle: Ibn Sahl, al-Qūhī et Ibn al-Haytham, Paris, Les Belles Lettres, 1993.
‒ 1996: Rashed, Roshdi, Math. inf. I.
‒ 1997: Histoire des sciences arabes, sous la direction de Roshdi Rashed avec la collaboration de Régis Morelon, Paris, Seuil, 1997, 3 v.
‒ 2000a: Rashed, Roshdi, Math. inf. III.
‒ 2000b: Rashed, Roshdi - Bellosta, Hélène, Ibrāhīm ibn Sinān. Logique et géométrie au Xe siècle, Leiden, E.J. Brill, 2000.
Sa῾idan 1984: Sa῾īdān, Aḥmad S., Taṯlīṯ al-zāwiya fī 'l-῾uṣūr al-islāmiyya, "Maǧalla ma῾had al-maḫṭūṭāt al-῾arabiyya", 28, 1984, pp. 99-137.