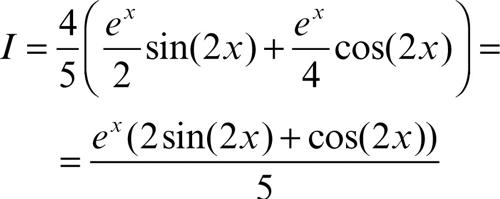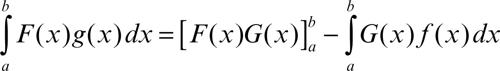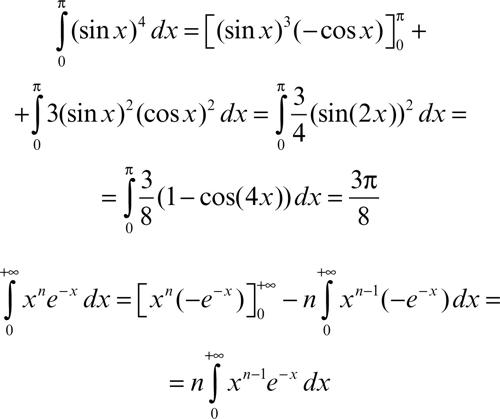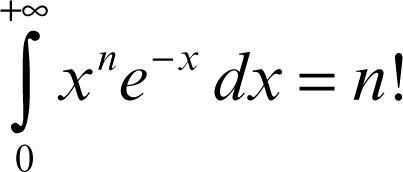integrazione per parti

integrazione per parti

integrazione per parti una delle tecniche standard per il calcolo di integrali indefiniti, applicabile a priori ogniqualvolta la funzione integranda goda di opportuna regolarità. Essa è espressa dalla relazione, equivalente alla regola di derivazione del prodotto,

dove F(x) e G(x) sono le rispettive primitive di ƒ(x) e g(x). La funzione F(x) si chiama fattore finito, il termine g(x)dx si chiama fattore differenziale. La decomposizione della funzione integranda nel prodotto Fg è dettata da due richieste: a) si deve conoscere una primitiva G di g; b) la funzione Gƒ deve essere più semplice da integrare della funzione originaria. Nel caso di polinomi e di funzioni esponenziali o trigonometriche, si tratta di funzioni facilmente integrabili, i cui integrali sono funzioni dello stesso tipo. Tuttavia, un polinomio si semplifica quando lo si deriva, per cui esso è un naturale candidato a essere fattore finito. Se invece sono presenti logaritmi o altre funzioni elementari inverse, le cui primitive non sono note, sono queste a dover essere assunte come fattore finito, perché le loro derivate sono razionali o algebriche. Per esempio (omettendo tutte le costanti di integrazione):

• I = ∫xsinxdx: con F(x) = x, g(x) = sinx si ha ƒ(x) = 1, G(x) = −cosx, e, quindi,

• I = ∫e^xcos(2x)dx: con F(x) = e^x, g(x) = cos(2x) si ha ƒ(x) = e^x, G(x) = (1/2)sin(2x). Perciò

L’integrale J = ∫sin(2x)e^xdx appare della stessa difficoltà di quello originario; integrando una seconda volta, con F(x) = e^x, g(x) = sin(2x), si ha:

che è l’integrale di partenza I. Sostituendo dunque si ha:

da cui

• I = ∫xlnxdx. Non si può assumere lnxdx come fattore differenziale, se non si conosce una primitiva di lnx; posto dunque F(x) = lnx, g(x) = x, si ha ƒ(x) = 1/x, G(x) = x ²/2. Pertanto

• I = ∫arctanxdx. Come sopra, si scelga

ottenendo

Il metodo si applica anche a integrali definiti, anche impropri, nella forma

utile soprattutto quando il termine finito F(x)G(x) si annulla (o ammette limite 0) in uno o entrambi gli estremi di integrazione:

Per induzione si deduce che: