infinito

infinito

Un tutto grande come le sue parti

Ci sono cose, come le stelle, che sono enormi o lontanissime se confrontate con gli oggetti della vita quotidiana; altre che sono invece piccolissime (come virus e atomi) e si possono vedere solo con sofisticati microscopi o con l'immaginazione. Tuttavia, il 'molto grande' o il 'molto piccolo' non raggiungono mai quella dimensione che chiamiamo infinito. Infinito significa infatti "che non ha fine". Ma che cos'è precisamente? Ed esiste qualcosa di infinito oppure, come lo scorrere ininterrotto dell'acqua nella cascata dipinta dall'artista olandese Cornelis Escher, l'infinito è solo frutto di un inganno e non lo si può nemmeno immaginare?

Infinitamente grande e infinitamente piccolo

Il primo esempio di infinito a cui solitamente si pensa proviene dalla matematica ed è quello dei numeri naturali: 1, 2, 3, 4, 5, … I puntini di sospensione significano che si può continuare all'infinito, aggiungendo sempre un nuovo numero. I numeri naturali sono infiniti proprio in questo preciso senso: comunque si pensi un numero 'grande', basta fare +1 per trovarne uno maggiore. Abbiamo così un esempio di infinitamente grande.

fig.

Consideriamo ora non soltanto i numeri naturali, ma anche quelli detti razionali, rappresentati da numeri decimali finiti o periodici. Considerando anche questi numeri, tra 0 e 1 ci sarà per esempio 0,5 intermedio tra i due. Ma anche tra 0 e 0,5 si può trovare un numero intermedio (continuo e discreto), come 0,25. Allo stesso modo, tra 0 e 0,25 si può trovare un numero intermedio, basta dividere 0,25 per 2 e si ottiene 0,125. Di nuovo, tra 0 e 0,125, dividendo per 2, si trova un numero intermedio. E così via, proseguendo all'infinito. Abbiamo qui un esempio di infinitamente piccolo (per questa proprietà i numeri razionali si dicono densi) (v. fig.).

Infinito potenziale e infinito attuale

Gli esempi precedenti non convincono però dell'esistenza di oggetti che abbiano davvero un numero infinito di elementi. In effetti, ciò che possiamo dire è, nel primo caso, che "si può sempre trovare un numero naturale più grande di un numero dato" e, nel secondo caso, che "si può sempre trovare un numero decimale positivo più piccolo di un numero dato". Si afferma perciò una potenzialità: la procedura si può ripetere quante volte si vuole per trovare numeri sempre più grandi o sempre più piccoli. In questo senso si parla di infinito potenziale, concetto accettato anche dal più influente degli antichi filosofi greci, Aristotele. Secondo Aristotele, invece, non potevano esistere oggetti o enti matematici con un numero di elementi davvero senza fine: il filosofo negava cioè che potesse esserci una realtà in atto infinita o, come si dice, un infinito attuale.

Paradossi

fig.

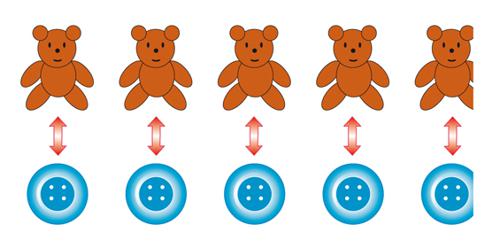
Che cosa significa affermare che due insiemi hanno lo stesso numero di elementi? Basterebbe contarli, per dirlo, ma anche se non si è capaci di contare lo si può stabilire. Per esempio due insiemi, uno di orsacchiotti e uno di bottoni, hanno lo stesso numero di elementi perché per ogni orsacchiotto c'è un bottone e, viceversa, per ogni bottone c'è un orsacchiotto (v. fig.).

In matematica, quando si può fare un accoppiamento del genere si dice che è stata stabilita una corrispondenza biunivoca. Così orsacchiotti e bottoni sono qui in corrispondenza biunivoca; e proprio per questo sono nello stesso numero.

Con la tecnica della corrispondenza biunivoca si possono allora confrontare insiemi infiniti e capire se hanno lo stesso numero di elementi. Consideriamo per esempio i numeri naturali e immaginiamo di scriverli tutti, in ordine crescente:

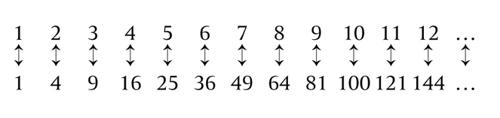
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 ...

Ora consideriamo i loro quadrati, i numeri cioè che si ottengono moltiplicandoli per sé stessi, e scriviamo anch'essi in ordine crescente:

1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144 ...

Tra questi due insiemi si può stabilire una corrispondenza biunivoca, come si vede se mettiamo i due insiemi vicini, come gli orsacchiotti e i bottoni.

L'aspetto paradossale di questa corrispondenza (che fu osservata per la prima volta da Galileo Galilei e per questo è nota come paradosso di Galilei) non consiste tanto nel fatto che i due insiemi abbiano lo stesso numero di elementi. Entrambi, infatti, sono infiniti. L'aspetto paradossale consiste nel fatto che i numeri quadrati sono una parte dei numeri naturali e quindi il tutto (i numeri naturali) ha lo stesso numero di elementi di una sua parte (i soli numeri quadrati). Viene meno una delle proprietà fino ad allora considerata indiscutibile, e cioè che "il tutto è maggiore di una sua parte".

In effetti, negli insiemi di oggetti di cui abbiamo esperienza, è sempre vero che il tutto è maggiore di una sua parte, ma ciò accade perché sono insiemi con un numero finito di elementi. Ciò che appariva paradossale a Galilei, alla fine del 19° secolo diventa, grazie al matematico tedesco Richard Dedekind, la definizione di insieme infinito, cioè un insieme che può essere messo in corrispondenza biunivoca con una sua parte propria.

Gli infiniti non sono tutti uguali

Esiste una gerarchia anche nell'infinito. Se così non fosse si potrebbe prendere come modello l'insieme dei numeri naturali e tutti gli insiemi infiniti potrebbero essere messi in corrispondenza biunivoca con esso. Alla fine del 19° secolo, invece, il tedesco Georg Cantor dimostrò che non tutti gli infiniti sono uguali!

Egli prese in considerazione tutti i numeri reali positivi compresi tra 0 e 1, cioè tutti i numeri maggiori di 0 ma minori di 1 che si possono scrivere in forma decimale come 0,1,… e dimostrò che questi numeri sono più di tutti i numeri naturali: la loro 'infinità' è d'ordine superiore. Non solo, ma con un procedimento matematico relativamente semplice mostrò che si possono costruire infinità sempre più grandi, 'infinite infinità', per così dire. In questo modo, l'infinito non era più soltanto definito in negativo, come qualcosa di non finito, ma si precisava la sua idea e si volgeva al plurale il concetto: si passava dall'infinito agli infiniti.

Ma esiste qualcosa di infinito?

Chiarito il significato di infinito dal punto di vista della matematica, su questo concetto rimangono aperti problemi scientifici di più larga portata. Per esempio, l'Universo è finito, infinito oppure non ha senso porsi la domanda?

C'è un'esperienza domestica di infinito. Se una persona si trova fra due specchi posti l'uno di fronte all'altro, su ognuno dei due si riflette l'immagine dell'altro e si vede l'immagine riflessa più e più volte: infinite volte da un punto di vista teorico. Nella pratica però le immagini diventano sempre più piccole e lontane, sempre meno nitide e luminose. È un infinito di fatto 'irraggiungibile'.

Anche per le dimensioni dell'Universo il discorso è simile. La fisica moderna avanza infatti l'ipotesi che l'Universo sia finito; ma la sua finitezza è così grande che i suoi estremi sono irraggiungibili e quindi,a tutti gli effetti, è come se fosse infinito. Che sia finito non significa tuttavia che sia limitato, cioè che esista qualcosa 'oltre' l'Universo. Anche la superficie sferica della Terra è finita, ma non è limitata da nulla se non da sé stessa. Accade così che se il concetto di infinito, come idea, è precisato dalla matematica, l'idea di infinito resta un problema aperto che la scienza non può risolvere in via definitiva.

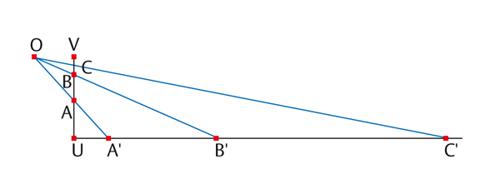
Un segmento ha lo stesso numero di punti di una semiretta!

fig.

Con la tecnica della corrispondenza biunivoca si può mostrare un altro paradosso dell'infinito: i punti di un segmento, anche piccolo, sono tanti quanti i punti di una semiretta. Infatti si può stabilire una corrispondenza biunivoca 'proiettando' i punti del segmento UV da un punto esterno, come O, sulla semiretta con origine nel punto U. Al punto A corrisponde A′, a B corrisponde B′ e così via (v. fig.).