identificabilità

identificabilita

identificabilità  Proprietà che un modello statistico deve soddisfare perché sia possibile condurre inferenza statistica (➔) circa i suoi parametri. Intuitivamente si afferma che un modello è identificabile se a ogni parametro θ corrisponde una e una sola distribuzione di probabilità per i dati.

Modello identificabile

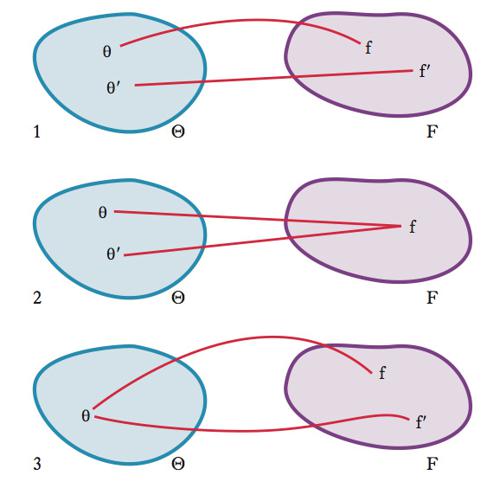
In modo più formale, dato un modello definito da una famiglia F={f(z;θ)} di distribuzioni di probabilità per i dati indicizzata da un parametro θ in uno spazio dei parametri Θ, si dice che tale modello è identificabile se esiste una corrispondenza biunivoca tra Θ e F, ovvero se a ciascun valore di θ corrisponde uno e un solo elemento di F (figura 1). La definizione formale di i. comprende sia il caso parametrico, in cui lo spazio dei parametri è finito-dimensionale (un vettore di parametri), sia il caso non parametrico, in cui lo spazio dei parametri è infinito-dimensionale (una funzione). Nel contesto di un modello parametrico regolare l’i. è assicurata dalla non singolarità della matrice di informazione di Fisher (➔ verosimiglianza massima, metodo della).

Modello non identificabile

Un modello non è identificabile quando la corrispondenza tra Θ e F non è biunivoca. Ci sono due casi in cui questo può accadere: il primo si ha quando più valori di θ sono compatibili con lo stesso elemento di F (figura 2); il secondo quando un particolare elemento di θ è compatibile con più elementi di F (figura 3).Per illustrare il primo caso, si consideri il modello lineare gaussiano (➔ gaussiana, distribuzione) con due regressori e un’intercetta: la distribuzione condizionata di Y∣X₁,X₂ è quella di una variabile aleatoria (➔) normale N(α+β₁X₁+β₂X₂,1). Si assuma che X₁ e X₂ siano due variabili dummy (➔ dummy, variabili), per es., che X₁ sia 1 per un maschio e 0 per una femmina, e X₂ sia 1 per una femmina e 0 per un maschio. Il modello parametrico è:

{f(y∣X₁=x₁,X₂=x₂;θ)∼N(α+β₁+(β₂−β₁)x₂,1), θ=(α,β₁,β₂)∈Θ},

dove x₁  e x₂ soddisfano x₁=1−x₂ per via della relazione X₁=1−X₂. In questo caso il modello presenta collinerità (➔) tra i regressori e il parame-tro θ=(α,β₁,β₂) non è identificabile. Infatti, esiste un numero infinito di vettori θ′=(α′,β′₁,β′₂), per i quali si ha f(y∣X₁=x₁,X₂=x₂;θ)=f(y∣X₁=x₁,X₂= x₂;θ′) per ogni x₁=1−x₂. Per illustrare il secondo caso si consideri una variabile Y gaussiana di varianza unitaria, ma con media uguale a μ_A e μ_B nelle due sottopopolazioni A e B. Si assuma, che la probabilità π di appartenere al gruppo B sia nota. Si ipotizzi, inoltre, che non sia possibile osservare il valore di Y per le unità che appartengono al gruppo B. Il parametro di interesse è la media μ=E(Y)=μ_Aπ+μ_B(1−π), la quale non è identificabile poiché non lo è la media μ_B per la sottopopolazione B. Un modo per affrontare questo problema è quello di reperire informazioni aggiuntive. Per es., se si potesse affermare che μ_B fosse compresa tra due valori noti c e d, allora se ne dedurrebbe che μ deve essere necessariamente compresa nell’intervallo

μ

_A+(c−μ_A)π≤μ≤μ_A+(d−μ_A)π,

di ampiezza (d−c)π.. Si parla in questo caso di identificazione per intervalli. Se il parametro di interesse è invece il vettore θ=(μ_A,μ_B), pur essendo θ non identificabile, si dice che esso è parzialmente identificabile, poiché è identificabile il sottovettore costituito dalla sola componente μ_A.