grafo
grafo
grafo struttura matematica descrivibile come un insieme di nodi e un insieme di archi che uniscono coppie di nodi. Un grafo è anche definibile a partire dal concetto di relazione in un insieme, intesa come corrispondenza dell’insieme in sé: esso rappresenta tale relazione evidenziando le corrispondenze tra i diversi elementi, ma è al contempo identificabile con essa. Per questo, matematicamente si definisce il grafo come un insieme in cui è definita una relazione tra i suoi elementi. Gli elementi sono rappresentati da punti, i nodi o vertici del grafo, mentre il fatto che per una coppia di elementi la relazione è vera è evidenziato da una linea che unisce i nodi interessati e che è detta arco o spigolo. Un grafo G risulta così essere una coppia di insiemi (X, A) dove X è l’insieme dei nodi e A è l’insieme degli archi. A risulta, quindi, un sottoinsieme del prodotto cartesiano X × X. Due nodi sono adiacenti se esiste un arco che li unisce; in termini generali, una sequenza di nodi adiacenti costituisce un percorso sul grafo.
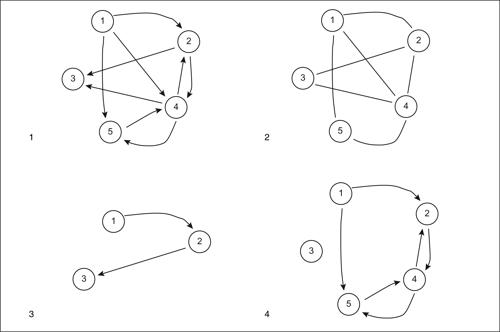
Un arco è definibile come coppia di nodi, suoi estremi: se è importante l’ordine con cui essi sono indicati, l’arco risulterà orientato e rappresenterà una relazione non simmetrica tra i nodi suoi estremi (graficamente sarà rappresentato da una freccia che ne indica l’orientamento, cioè il senso di percorrenza). Due archi si dicono adiacenti se hanno uno (e uno solo) dei due estremi in comune. Un grafo orientato è un grafo che ha almeno un arco orientato; per tale arco è rilevante l’orientamento, mentre gli altri possono essere percorsi in entrambi i versi. In figura 1 è rappresentato un grafo (totalmente) orientato, mentre in figura 2 uno non orientato. Una rete ferroviaria può essere considerata un grafo non orientato, mentre un albero genealogico è un grafo orientato (dal genitore al figlio). Il grafo in figura 1 è così descrivibile: G = (X, A), X = {1, 2, 3, 4, 5}, A = {(1, 2), (1, 4), (1, 5), (2, 3), (2, 4), (4, 2), (4, 3), (4, 5), (5, 4)}; il grafo in figura 2 è invece così descrivibile: G′ = (X, A′), X = {1, 2, 3, 4, 5}, A′ = {(1, 2,), (1, 4), (1, 5), (2, 1), (2, 3), (2, 4), (3, 2), (3, 4), (4, 2), (4, 3), (4, 5), (5, 1), (5, 4)}. Un grafo (orientato o non orientato) tale che per ogni coppia di nodi esiste un arco che li collega è detto completo.
In generale, su ciascun nodo può incidere un numero arbitrario di archi; tale numero ne rappresenta in qualche misura la complessità e prende il nome di grado (o anche ordine o valenza) del nodo. Si definisce il grado massimo e il grado minimo di un grafo, come il massimo (rispettivamente, il minimo) dei gradi dei suoi nodi (→ grafo, nodo di un); se i nodi hanno tutti lo stesso grado n, tale valore n è detto grado del grafo.
Nel caso di grafo orientato si preferisce distinguere tra archi entranti e archi uscenti dal nodo e definire così, per ogni nodo, un grado entrante e un grado uscente.
Un sottografo S di un grafo G(X, A) indotto da un insieme Y ⊆ X è un grafo S = (Y, B) in cui l’insieme degli archi è
Prendendo come esempio il grafo orientato in figura 1, il sottografo di G indotto da Y = {1, 2, 3} è rappresentato in figura 3. In altri termini, si dice sottografo relativo a un insieme di punti il grafo costituito da tali punti e dagli archi che li connettono. Si dice invece grafo parziale di G, qui indicato con P = (X, C), il grafo che si ottiene da G considerando un sottoinsieme dei suoi archi: C ⊆ A; in altri termini, è un grafo che contiene tutti i nodi, ma un numero minore (o uguale) di archi che li connettono. In figura 4 è rappresentato il grafo parziale definito dal sottoinsieme di archi C = {(1, 2), (1, 5), (2, 4), (4, 2), (4, 5), (5,4)}.
Un esempio elementare di grafo è una carta della rete stradale: i nodi o vertici sono le città e gli archi o spigoli sono le strade; considerando le strade a senso unico il cammino è semplice, mentre le strade a doppio senso di circolazione rappresentano cammini composti. La carta delle sole autostrade costituisce un grafo parziale; la carta delle strade di un sola regione è un sottografo; la carta della autostrada di una regione è un sottografo parziale.
Una catena in un grafo G, indicata con K, è un suo sottografo parziale (che quindi ha contemporaneamente le caratteristiche di un sottografo e di un grafo parziale) definito da un sottoinsieme di archi
e un sottoinsieme di nodi {x1, x2, x3, …, xk} tali da costituire una sequenza finita di nodi e archi adiacenti x1, a1, x2, a2, …, xk−1, ak−1, xk, in cui quindi aj = (xj, xj+1) oppure (xj+1, xj) con j = 1, 2, 3, ..., k − 1; una catena chiusa (tale cioè che x1 = xk), in cui l’estremo iniziale del primo arco e l’estremo finale dell’ultimo arco coincidono, è detta circuito.
Un cammino in un grafo orientato G è una particolare catena in cui, nella definizione precedente, si abbia aj = (xj, xj+1) con j = 1, 2, 3, ..., k − 1. In altri termini, ciò che distingue un cammino da una catena è l’esistenza dell’orientamento degli archi. Una catena è, infatti, un cammino non orientato. Un cammino chiuso ha il nodo x1 = xk; un cammino chiuso in cui l’unico nodo ripetuto è il primo è detto ciclo. Poiché si definisce semplice un cammino in cui non vi siano archi ripetuti ed elementare uno in cui non vi siano nodi ripetuti, un ciclo è un cammino elementare dal nodo x1 al nodo xk unito all’arco (xk, x1). Notevole importanza per le loro applicazioni pratiche rivestono due particolari cicli: il → ciclo hamiltoniano e il → ciclo euleriano. Un particolare tipo di grafo, privo di ciclicità, è invece l’→ albero.
Un grafo G = (X, A) si definisce connesso se per ogni coppia di nodi xi, xj ∈ X esiste una catena da xi a xj; se tale catena è un cammino, il grafo è detto fortemente connesso. Visivamente, un grafo è connesso se non ha nodi isolati e, in caso di grafo orientato, è fortemente connesso se ogni suo nodo è raggiungibile da qualsiasi altro nodo. Un couplage di un grafo è un insieme di archi che a due a due non hanno estremi in comune.
In un grafo, dati due nodi xi e xj si può considerare il numero minimo di archi necessario per costruire una catena che li colleghi (si tratterà di cammini nel caso di grafo orientato); indicato con d(xi, xj) tale numero, il suo valore massimo, al variare di xi e xj nell’insieme X dei nodi del grafo è detto diametro D del grafo: D = max d(xi, xj). Conseguentemente, il nodo (o i nodi) per cui è minimo il valore
è detto centro del grafo e se xk è il nodo centro (o uno dei nodi centro) il valore R(xk) è detto raggio del grafo. In un grafo orientato, dati due nodi xi e xj, si considera a volte la minima lunghezza (cioè il minimo numero di archi) di un cammino dal nodo xi al nodo xj: a tale valore viene dato il nome di scarto del nodo xi dal nodo xj; se non esiste un cammino che va dal primo al secondo nodo considerati, lo scarto è ∞. Si definisce poi nucleo di un grafo orientato G(X, A) un insieme N ⊆ X tale che, preso un qualsiasi xk ∈ X, si ha: se xk ∈ N allora xk non ha successori in N, altrimenti esiste in N almeno un suo successore.
Queste caratteristiche di un grafo sono facilmente intuibili attraverso la sua rappresentazione visiva come rete di nodi e di archi. Anche altre proprietà dei grafi sono desumibili dallo schema visivo che si associa a ciascuno di essi. In particolare si dice che un grafo è:
• planare se è possibile disegnarlo su un piano in modo che gli archi abbiano come soli punti comuni i vertici (gli archi, cioè, non si intersechino);
• semplice se non ha archi multipli, cioè archi che collegano la stessa coppia di nodi, né ha archi che collegano un nodo con sé stesso (detti loop); un grafo orientato è quindi semplice se per ogni coppia di archi a = (xi, xj) e b = (xm, xn) valgono le relazioni: xi ≠ xj, xm ≠ xn e (xi ≠ xm ∨ xj ≠ xn). Se non è semplice il grafo è detto composto;
• bipartito se l’insieme dei suoi nodi può essere separato in due partizioni P1 e P2 tali che per ogni arco (xi, xj) ∈ A si ha che o xi ∈ P1 e xj ∈ P2 oppure xi ∈ P2 e xj ∈ P1.
Il grafo commutato di un grafo G(X, A) è il grafo G′ (A, X) che ha per nodi gli archi di G e tale che a1 e a2 sono collegati da un elemento di X se e solo se in G hanno un estremo comune.
Ai nodi di un grafo può essere assegnata una colorazione in modo tale che a due nodi adiacenti non sia mai assegnato lo stesso colore: da questa assegnazione nasce il problema di quale sia il minimo numero di colori necessari per colorare un grafo (→ quattro colori, problema dei); tale numero è detto numero cromatico del grafo.
Per l’omomorfismo e l’isomorfismo tra grafi si vedano, rispettivamente, le voci → omomorfismo e → isomorfismo.
☐ Grafo numerato e grafo poligonale. Dato un grafo G(X, A), l’insieme X dei suoi nodi, essendo finito e, per esempio, di cardinalità n, può essere messo in corrispondenza biunivoca con i primi n numeri naturali (diversi da 0). È, quindi, possibile numerare i suoi vertici da 1 a n e considerare l’insieme X come insieme {1, 2, ..., n}.
Se G′ è un grafo planare privo di archi che si intersecano, esso divide il piano in regioni dette facce del grafo. Se il grafo G è semplice, planare, connesso e ha la proprietà che ogni arco è confine di due differenti facce, allora il grafo è detto poligonale. In un grafo poligonale il numero ν dei nodi (detti anche vertici), quello s degli archi (o spigoli) e quello ƒ delle facce sono legati dalla relazione di → Eulero.
☐ Grafo topologico. È un grafo avente per nodi punti di una superficie e per archi linee congiungenti a due a due tali nodi, con la condizione che due archi non abbiano intersezioni all’infuori di quelle che provengono da un eventuale nodo in comune; in questo caso il grafo è tracciato sulla superficie. Un grafo si dice tracciabile su una superficie S se è isomorfo (→ isomorfismo) a un grafo topologico tracciato su S: un grafo planare è tracciabile su un piano (tale proprietà vale per un grafo qualsiasi e non soltanto per un grafo topologico). Un grafo planare finito è isomorfo a un grafo finito tracciabile su una superficie sferica.
La considerazione di grafi topologici tracciabili su superfici diverse dal piano porta a differenti valutazioni del numero cromatico di un grafo. Un grafo planare ha come massimo numero cromatico 4 (il citato problema dei quattro colori); lo stesso, dato l’isomorfismo sopramenzionato, avviene per un grafo tracciabile su una sfera: in nessun caso occorrono cinque colori. Il problema è stato formulato e risolto anche per grafi tracciabili su superfici più complesse: è noto, per esempio, un grafo tracciabile su un toro che richiede sette colori, ma si può affermare che il numero cromatico di un grafo tracciabile su un toro non supera 7.