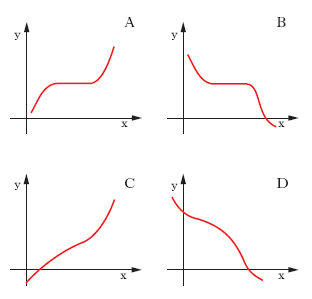
monotona, funzione
monotona, funzione In matematica, una funzione f(x), reale di una variabile reale, si dice m. se per ogni coppia di valori x′, x″ del suo insieme di definizione, per la quale sia x′<x″, risulta f(x′)≤f(x″) (funzione m. non decrescente; fig. A), ovvero f(x′)≥f(x″) (funzione m. non crescente; fig. B); se, in particolare, le disuguaglianze valgono in senso stretto, escludendosi cioè che per x′≠x″ risulti f(x′)=f(x″), si parla, rispettivamente, di funzione crescente e decrescente (fig. C e D, rispettivamente). Le funzioni m. sono dotate di funzione inversa univoca. È m., per es., la funzione y=x2 per x≥0 (la funzione inversa è x=√‾‾‾y per y≥0). Inoltre, se una funzione m. è derivabile in un intervallo, la sua derivata ha ivi segno costante, riuscendo f′(x)≥0 se f(x) è non decrescente oppure crescente; f′(x)≤0 se f(x) è non crescente oppure decrescente.
Per una successione a1, a2,... an,... di numeri reali, valgono le analoghe definizioni e denominazioni: se an≤an+1, la successione si dice m. non decrescente; se an<an+1, crescente; se an≥an+1, non crescente; se an>an+1, decrescente. In ogni caso una successione m. ammette limite, finito o infinito.