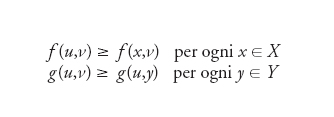equilibrio di Nash
equilibrio di Nash
Per studiare le situazioni in cui gli interessi dei giocatori non sempre sono contrapposti, e che sono le più interessanti dal punto di vista delle applicazioni, John von Neumann e Oskar Morgenstern hanno introdotto la teoria cooperativa. Qualche anno dopo, riprendendo e ampliando un’idea di Antoine Augustin Cournot, John F. Nash jr ha formalizzato l’idea di gioco non coopera-tivo in forma strategica (o normale) e di equili-brio associato, che da allora viene chiamato equilibrio di Nash. Un gioco (non cooperativo, in forma strategica, a due persone) è il dato di X,Y e f,g:X×Y→ℝ, dove X e Y sono gli spazi delle strategie dei due e f e g le loro funzioni di utilità. Un equilibrio del gioco è rappresen-tato da una coppia di strategie (u,v), u∈X, ν∈Y, tali che
In altre parole, nessuno dei due giocatori ha interesse a deviare dalla coppia proposta, dando per scontato che l’altro si adegui alla prescrizione. Nash dimostra poi, nella sua tesi di dottorato dove ha definito il modello, un teorema di esistenza per equilibri in strategie miste di giochi finiti. Non è difficile vedere che il procedimento dell’induzione a ritroso che si utilizza per analizzare gli esiti dei giochi finiti a informazione perfetta porta a equilibri di Nash, così come sono equilibri di Nash i punti sella dei giochi strettamente competitivi (a somma zero). Nel caso di giochi in forma estesa, l’idea di equilibrio è stata raffinata, portando a concetti più restrittivi (equilibrio trembling hand, perfetto, sequenziale). Una generalizzazione importante è l’idea di equilibrio correlato, introdotta da Robert Aumann (premio Nobel per l’Economia nel 2005), e di strategia evolutiva stabile, introdotta da John Maynard Smith in contesto biologico. Il concetto di equilibrio di Nash è utilizzato in moltissime applicazioni nei campi più disparati, e rappresenta la definizione di razionalità che la matematica propone in presenza di decisioni interattive.