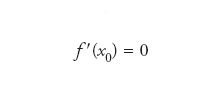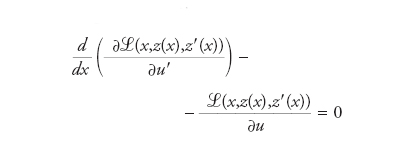equazione di Euler-Lagrange
equazione di Euler-Lagrange
Per funzioni reali di variabile reale f: ℝ→ℝ una condizione necessaria per avere un massimo o un minimo in un punto x0 dove f è derivabile, è che x0 risolva l’equazione
Consideriamo ora un funzionale del tipo F(u)=∫βαℒ(x,u(x),u′(x))dx dove le funzioni ℒ:ℝ3→ℝ (lagrangiana) e u:[a,b]→ℝ sono regolari e inoltre, dati α,β∈ℝ, valgano agli estremi dell’intervallo [a,b] le condizioni u(a)=α, u(b)=β. Condizione necessaria affinché z(x) (nella classe di funzioni considerata) sia un massimo, un minimo o più in generale un punto critico per il funzionale F, è che z risolva l’equazione di Euler-Lagrange
Al di là dell’analogia con la precedente, l’importanza di questa equazione differenziale (che si estende al caso di funzionali più generali) risiede nella corrispondenza che s’instaura tra soluzioni di equazioni differenziali, una volta intese in senso opportuno, e punti critici di funzionali.
→ Analisi non lineare: metodi variazionali; Variazioni, calcolo delle