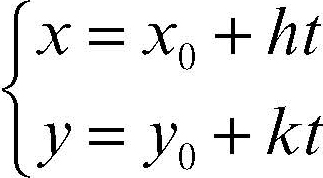coefficiente angolare
coefficiente angolare
coefficiente angolare numero che indica una direzione in un sistema di riferimento cartesiano. In una retta di equazione y = mx + q è il valore del parametro m che appare come coefficiente della x. Il suo valore è legato all’inclinazione della retta rispetto all’asse delle ascisse e, considerati un qualunque incremento delle ascisse Δx = x2 – x1 e il corrispondente incremento delle ordinate Δy, è, per la retta, il rapporto costante m = Δy/Δx interpretabile come rapporto tra “incremento verticale” e “incremento orizzontale”. In termini goniometrici, si ha m = tanα, essendo α l’angolo formato dalla retta con la direzione positiva dell’asse delle ascisse x.
Intendendo la retta come grafico di una funzione, il coefficiente angolare è la derivata prima della funzione che descrive la retta, che risulta costante, trattandosi della derivata di un polinomio di primo grado.
Se la retta è assegnata mediante equazioni parametriche
il coefficiente angolare è dato dal rapporto k/h. Se la retta è assegnata mediante due suoi punti A1(x1, y1) e A2(x2, y2) il coefficiente angolare è dato da
Se la retta è rappresentata da un’equazione in forma implicita ax + by + c = 0, con b ≠ 0, il coefficiente angolare è −a/b. Il coefficiente angolare è positivo se e solo se la retta è crescente (nella direzione delle x crescenti), negativo se e solo se la retta è decrescente, nullo se la retta è parallela all’asse delle ascisse (e rappresenta perciò una funzione costante). Il coefficiente angolare non è definito per le rette parallele all’asse delle ordinate. Nel caso di una funzione derivabile y = ƒ(x), la sua derivata per x = x0 ha una interpretazione che coinvolge il concetto di coefficiente angolare: essa infatti indica il coefficiente angolare della tangente al grafico della funzione nel suo punto (x0, ƒ(x0)).